地图投影

地图投影

rygdsddssd God
  2023-03-14 17:17:07 2023-03-14 17:17:07 创建   2023-04-01 16:44:44 2023-04-01 16:44:44 更新      3.6k 字  12 分钟  

地图投影基本概念介绍

什么是地图学的数学基础？

地图的数学基础，是指使地图上各种地理要素与相应的地面景物之间保持一定对应关系的经纬网、坐标网、大地控制点、比例尺等数学要素。

  • 两个矛盾：
    • 一个是大（详）与小（略）的矛盾。——比例尺
    • 一个是球面与平面之间的矛盾。——经纬网、坐标网、大地控制点——地图投影

大地基准面

大地基准面（Datum）是利用特定椭球体对特定地区地球表面的逼近，椭球形态由椭球体参数确定。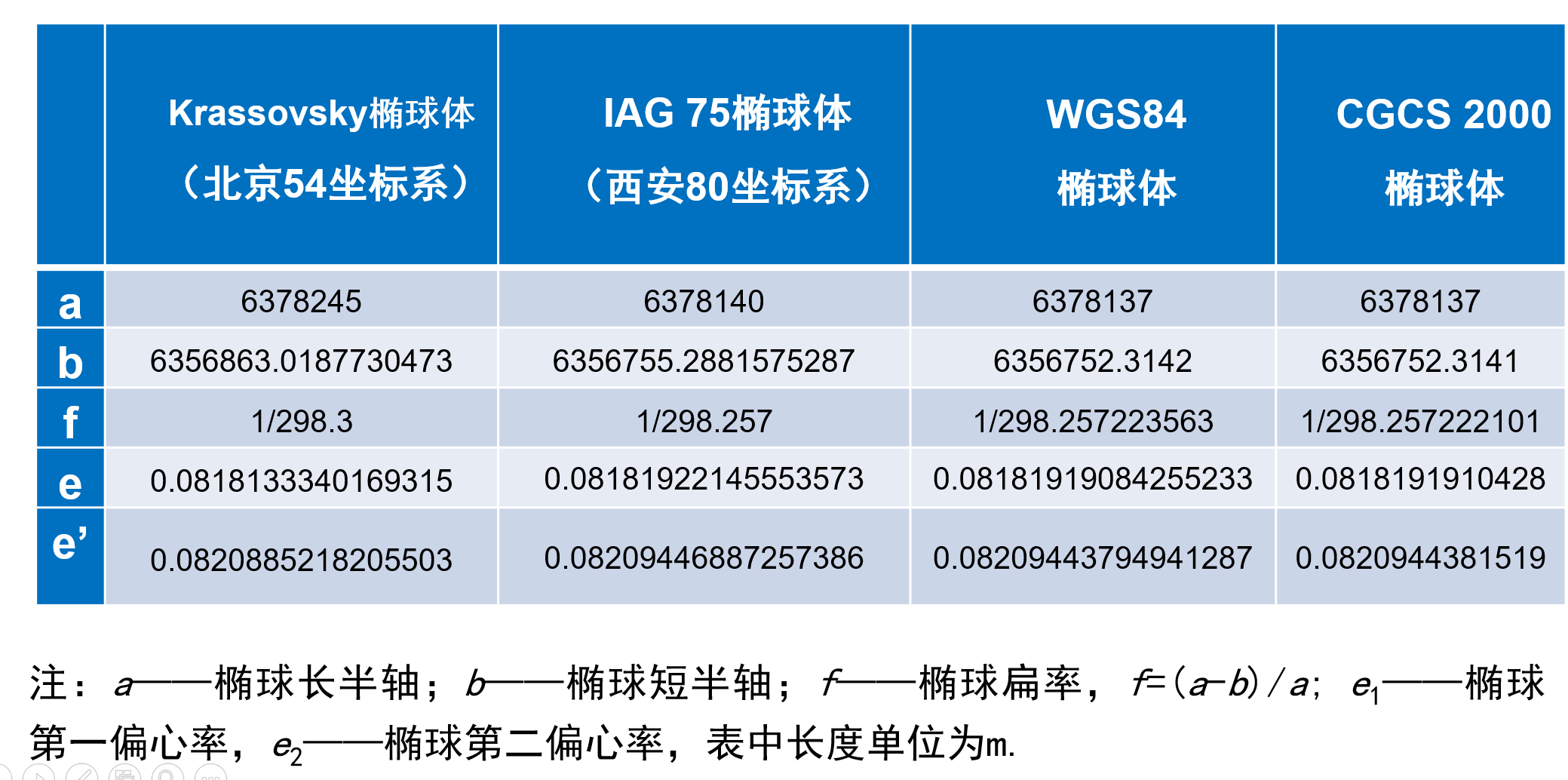
椭球体参数

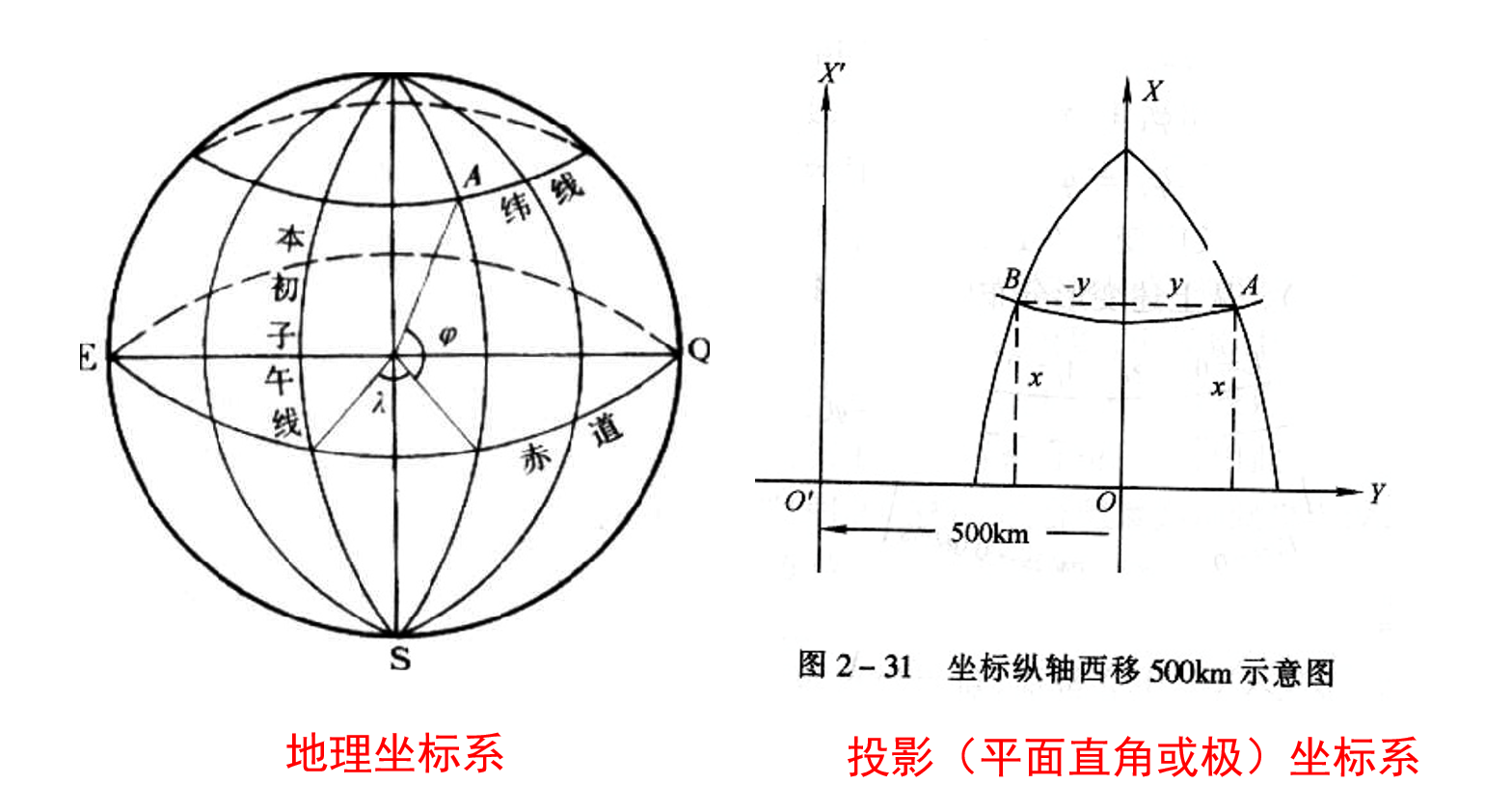
地理坐标系与投影坐标系

地理坐标系与投影坐标系

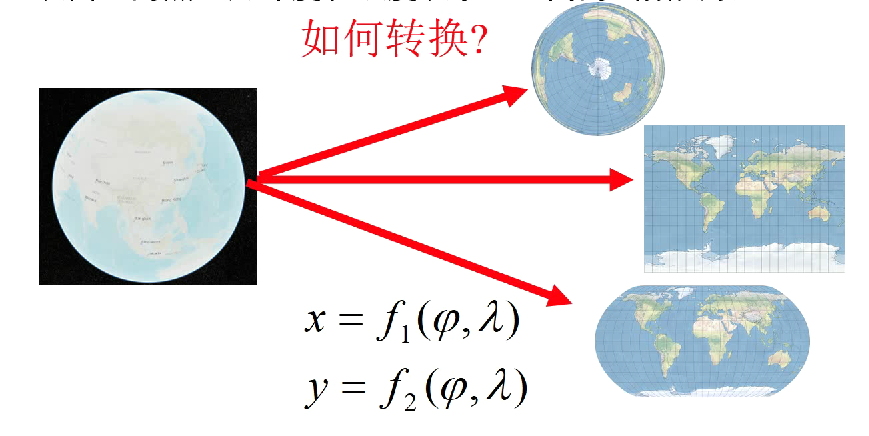
投影的实质和定义

建立平面上的点（用平面直角坐标或极坐标表示）和地球表面上的点（用纬度和经度表示）之间的函数关系。

投影的实质和定义

我国常用地图投影

高斯-克吕格投影————横轴等角椭圆柱投影

应用: 我国基本比例尺地形图≥1:50万的地形图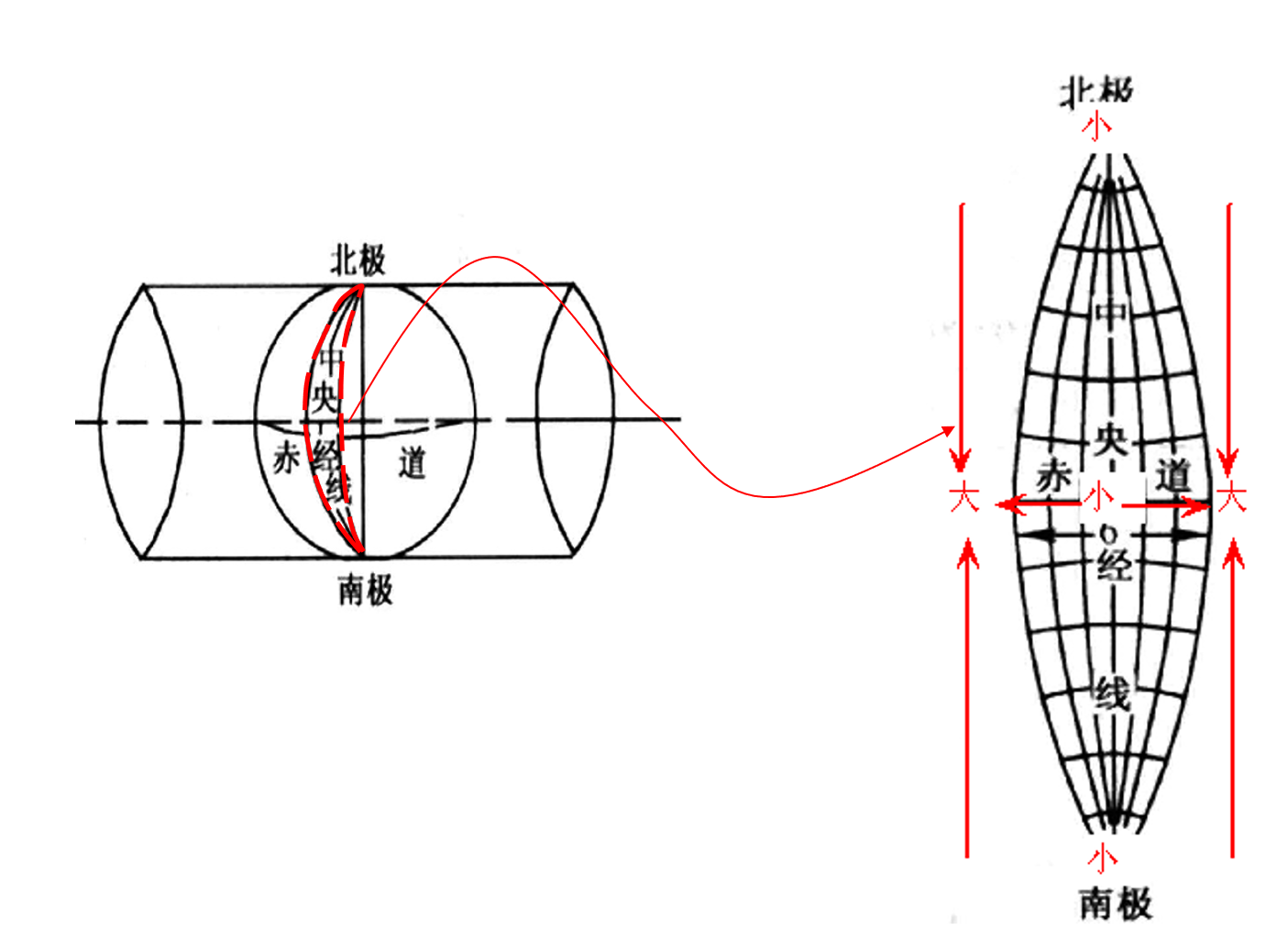
高斯-克吕格投影

  • 中央经线上无长度变形，长度比等于1，其它经线上长度比大于1，长度变形为正
  • 沿纬线方向，离中央经线越远，长度变形越大
  • 沿经线方向，纬度越低，长度变形越大。
  • 最大变形位于赤道与边纬的交点上，6度带最大长度变形为0.138%，最大面积变形为0.27%.

Lambert投影————双标准纬线正轴等角圆锥投影

应用: 我国新编1:100万地形图采用该投影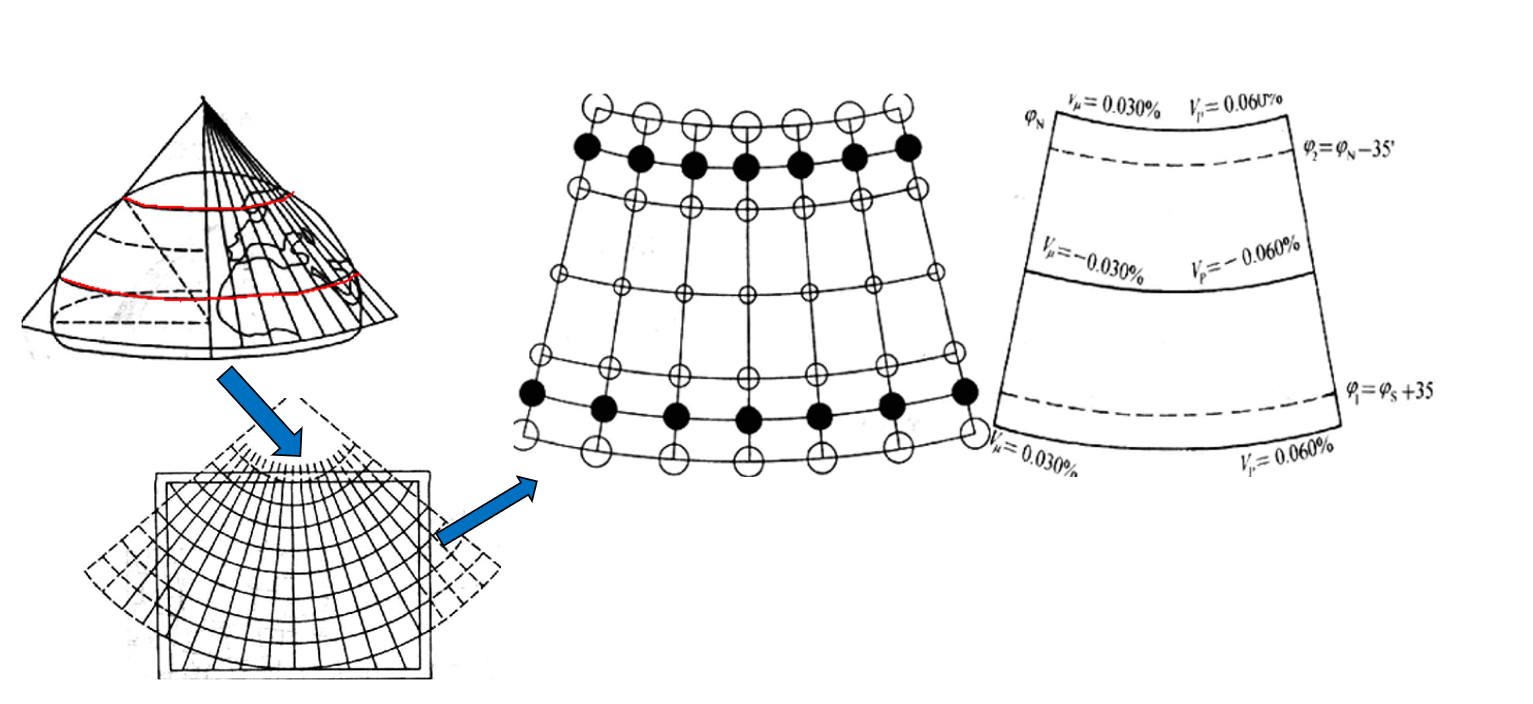
Lambert投影

  • 没有角度变形，等变形线与纬线一致
  • 两条标准纬线上没有变形
  • 同一经线上，两标准纬线外侧为正变形（长度比大于1），而内侧为负变形
  • 同一纬线上，等经差的线段长度相等，两条纬线之间的经线长度处处相等

中国地图一般采用正轴等面积（Albers）或等角圆锥投影

中国地图
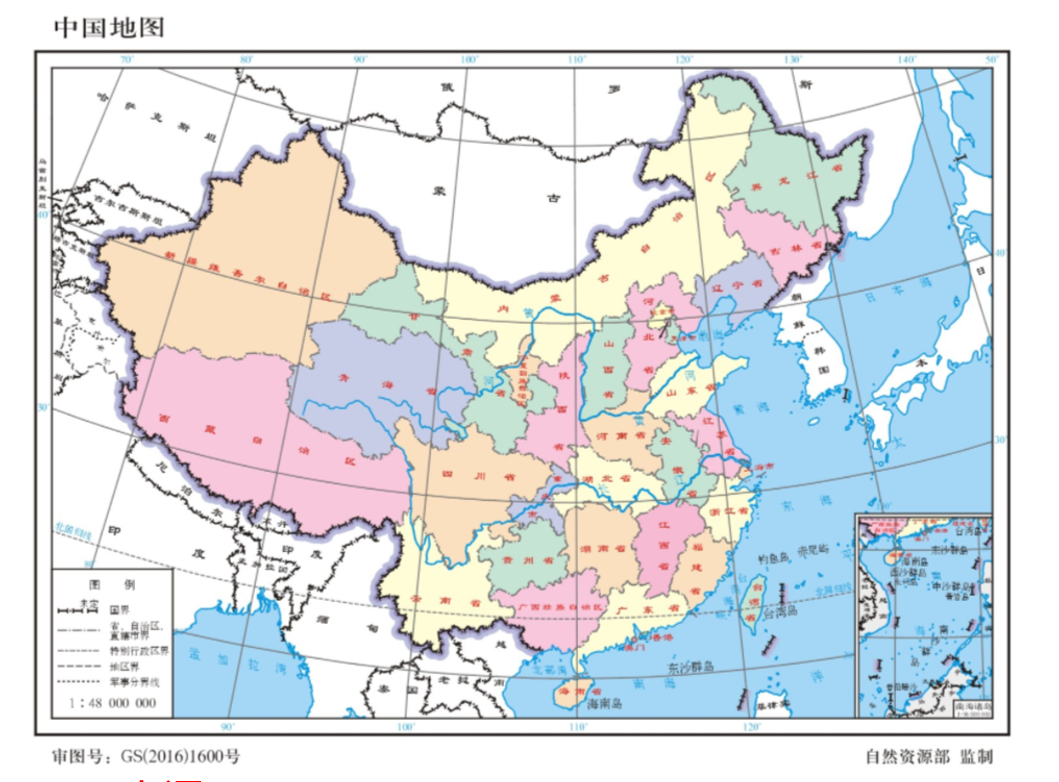
http://bzdt.ch.mnr.gov.cn/index.html

本次实验总体目标

  • 掌握地图投影的基本概念和地图投影判别的基本方法；
  • 掌握ARCGIS地图投影定义、投影转换、投影参数设置的基本操作方法；
  • 理解常用地图投影的数学原理，熟悉常用地图投影计算方法的编程实现过程。

地图投影判读实验

实验目的
  • 掌握地图投影判读的基本方法
  • 加深对地图投影的概念、投影变形性质等内容的理解
  • 加强对常用地图投影经纬网形状变化特点的了解
  • 能够快速判别出地图投影的类别和变形性质

投影判读的基本方法

往往是针对正轴投影
这是正轴圆柱投影，它的经纬线分布的很规律，相互垂直相交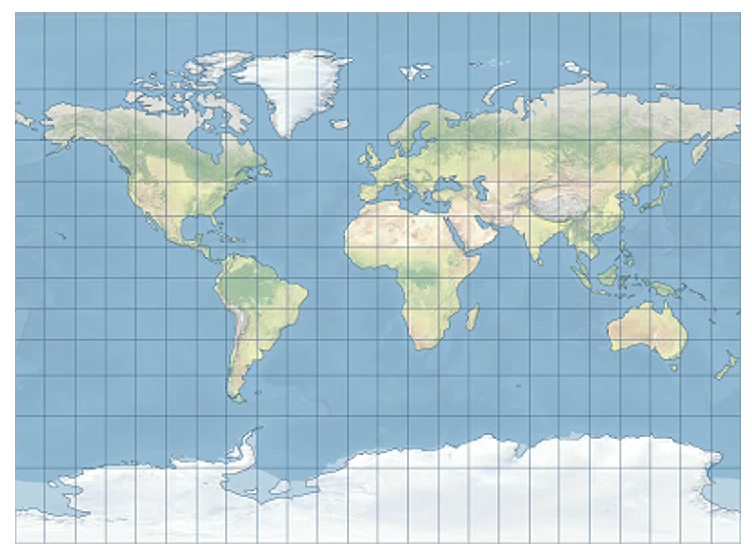
正轴圆柱投影
这是以极地伟投影范围，地极为投影中心的正轴方位投影

对于方位投影来说，如何判别

  • 分布在等差纬线的经线段长度是否相等
  • 同样的也是看经线段，是否是是从极地到赤道逐渐变长的

如若图中逐渐变小，就是等面积

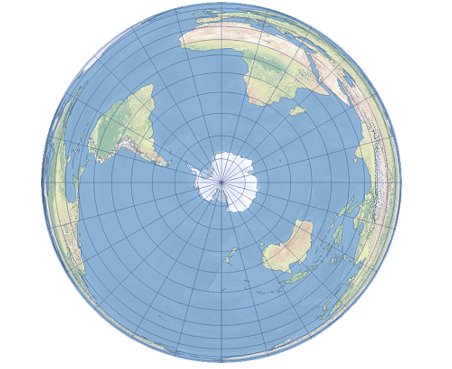
正轴方位投影

像扇子
纬线是同心圆弧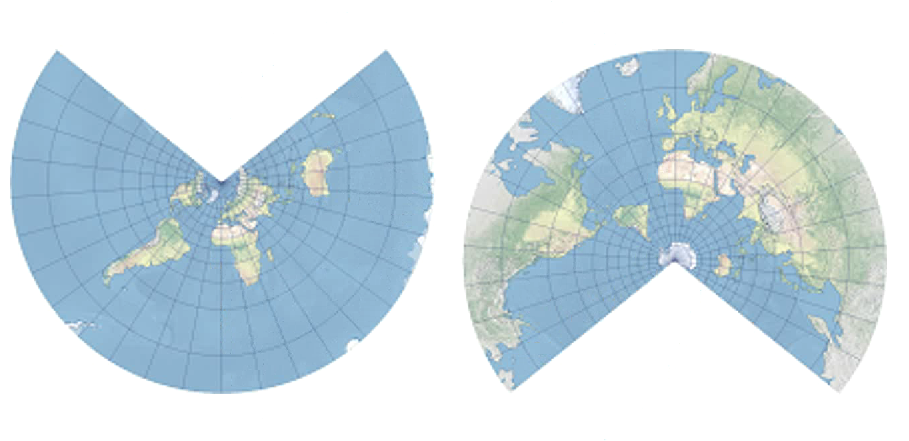
圆锥投影

常见投影的基本特征

每种投影有不同适用的区域，因为她的变形特点不一样嘛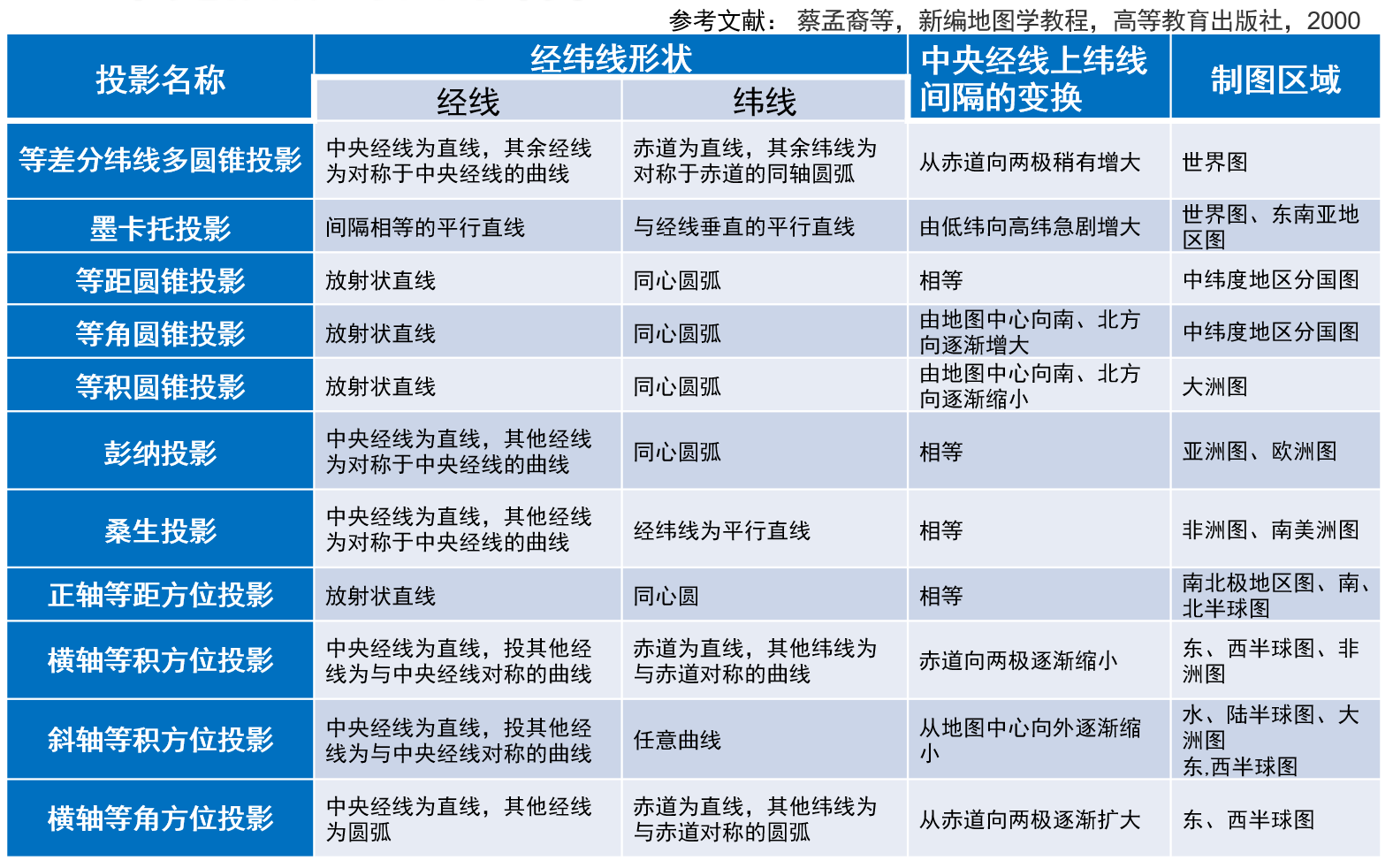
常见投影的基本特征

常见一些地图投影的经纬线形状特征

比如这个：

彭纳投影

彭纳投影

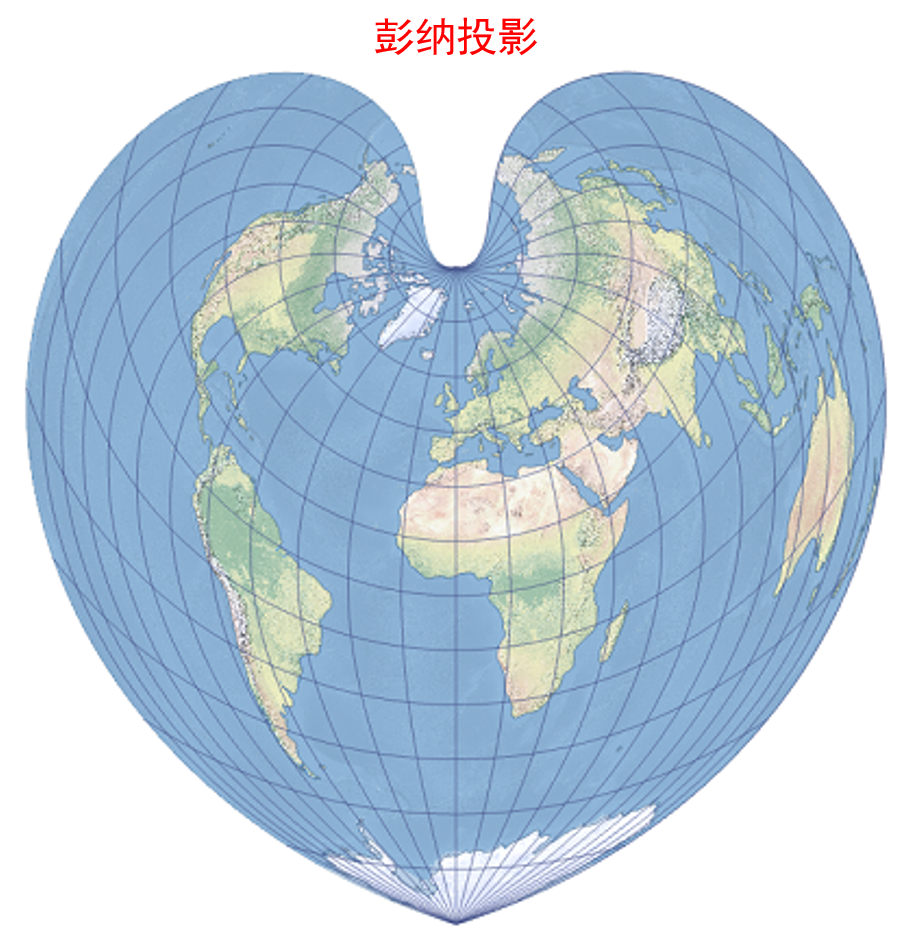
它是一个伪圆锥投影

特点
  • 中央经线为直线，其他经线为对称于中央经线的曲线
  • 纬线与经线交叉的同心圆弧
  • 中央经线上纬线间隔相等
  • 常用于亚洲图、欧洲图

只要纬线是同心圆弧，你就可以说他是一个圆锥投影，哪怕她长得像个桃心

地图投影判读作业

题目

（1）属正轴等积方位投影的是其中的哪一幅地图？沿其经纬线方向的变形特点如何？
（2）属正轴等距方位投影的是其中哪一幅地图？沿其经纬线方向的变形特点如何？
（3）属正轴等积圆锥投影的是其中哪一幅地图？沿其经纬线方向的变形特点如何？
（4）属正轴等角方位投影的是其中哪一幅地图？沿其经纬线方向的变形特点如何？
（5）属正轴等积圆柱投影的是其中哪一幅地图？沿其经纬线方向的变形特点如何？
（6）属墨卡托投影的是其中哪一幅地图？如果要在该投影上绘制澳大利亚的堪培拉（Canberra）到秘鲁的利马（Lima）的等角航线，应该如何绘制？沿着等角航线它们之间的距离是多少？

作业

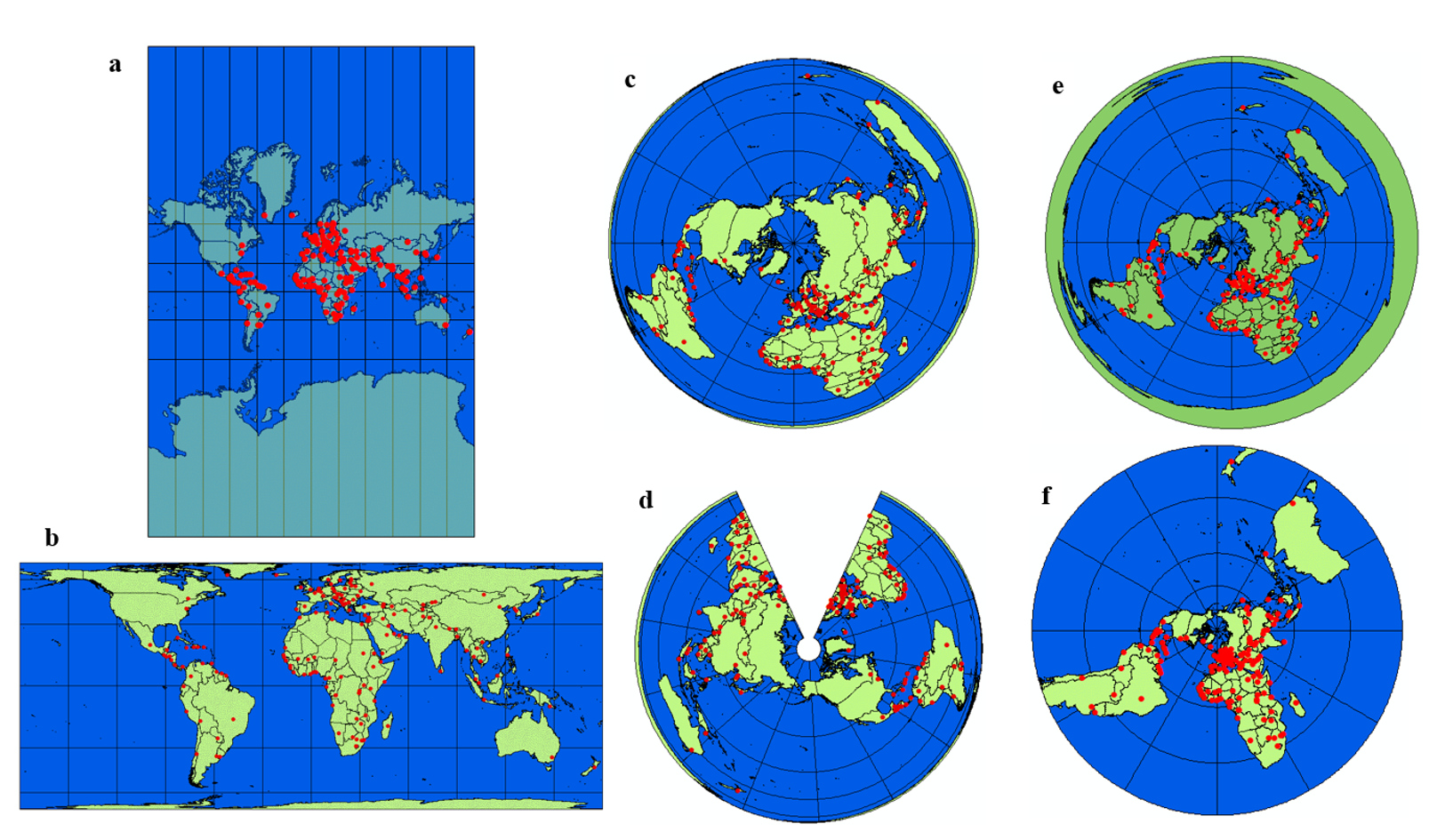
答案
（1）c

经线：放射状直线，纬线：同心圆，中央经线上纬线间隔的变化：从两极向赤道逐渐减小

（2）e

经线：放射状直线，纬线：同心圆，中央经线上纬线间隔的变化：相等

Azimuthal Equidistant 等距方位投影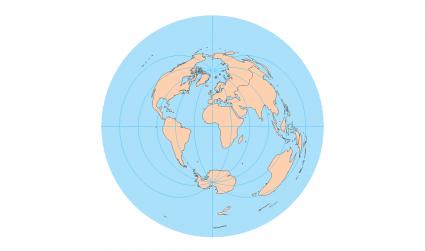
答案
等距方位投影可以保留距中心点的距离和方向。将地球上的所有点投影到一个平面上。虽然所有投影方法（赤道投影、极方位投影和斜轴投影）均可用，但使用频率最高的是极方位投影，这种投影会将所有经线和纬线划分为相等的部分，以保持等距离属性。
据说这种投影最初是埃及人绘制星图时使用的。

（3）d

经线：放射状直线，纬线：同心圆弧，中央经线上纬线间隔的变化：由地图中心向南北方向逐渐缩小

（4）f

经线：放射状直线，纬线：同心圆，中央经线上纬线间隔的变化：从两极向赤道逐渐增大

（5）b

经线：间隔相等的平行直线，纬线：与经线垂直的平行直线，中央经线上纬线间隔的变化：从赤道向两级逐渐增大

圆柱等积投影可将世界呈现为一个矩形，同时保持地图上的相对面积。瑞士数学家 Johann H.Lambert 于 1772 年首次描述了这种投影。自那以后许多年，出现了多种变体。该投影适合绘制赤道附近地区的大比例地图，且一般不建议用于绘制小比例（世界）地图。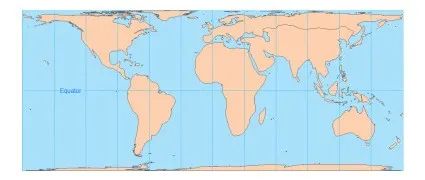
答案

贝尔曼投影

Behrmann 贝尔曼投影
贝尔曼投影是圆柱等积地图投影的一种，其标准纬线设置为南北纬 30°。
由于其等积的属性,它可以高度压缩极地地区。

（6）a

经线：间隔相等的平行直线，纬线：与经线垂直的平行直线，中央经线上纬线间隔的变化：从赤道向两级逐渐增大

右键打开属性表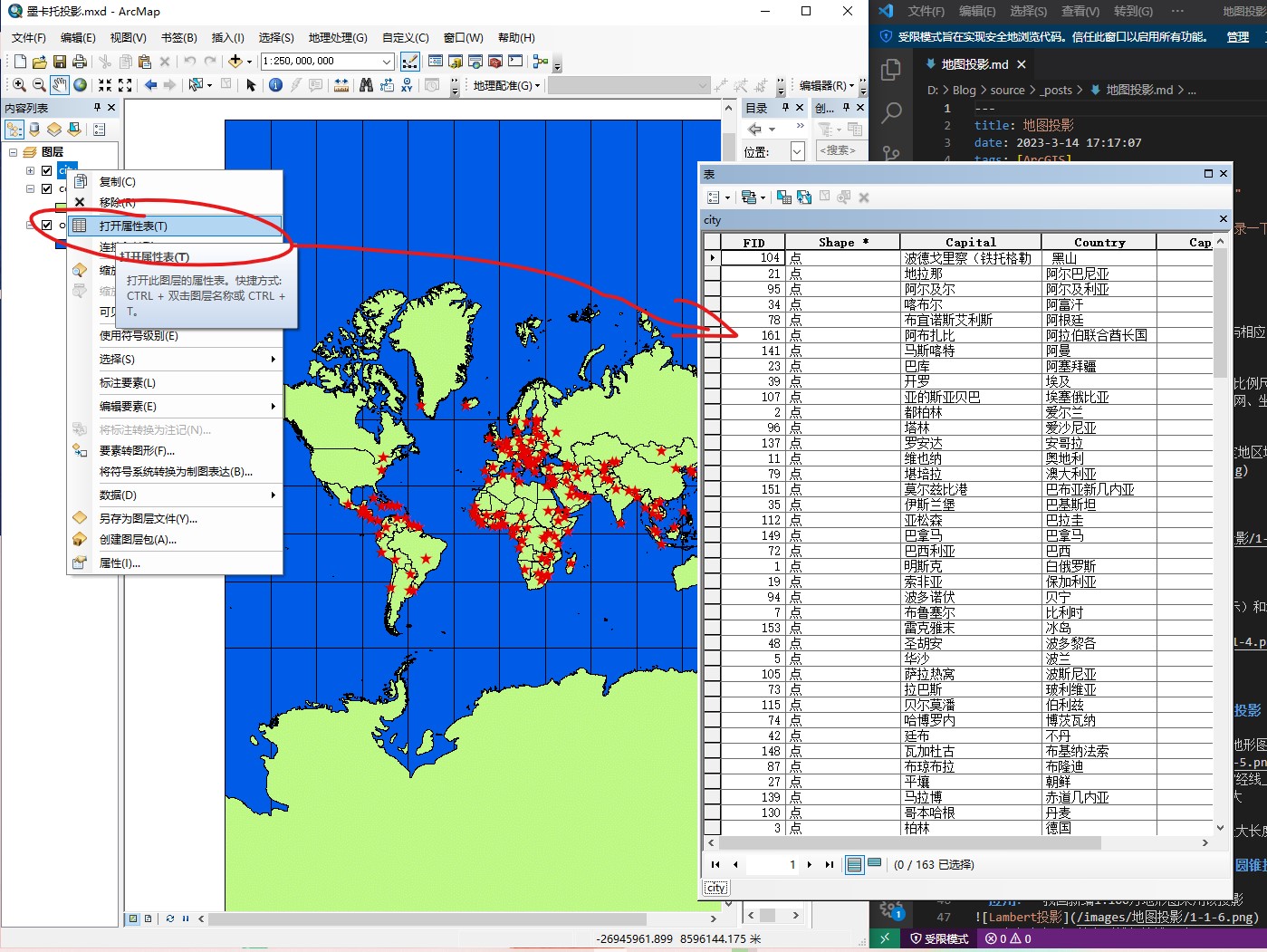
答案
双击这里可以聚焦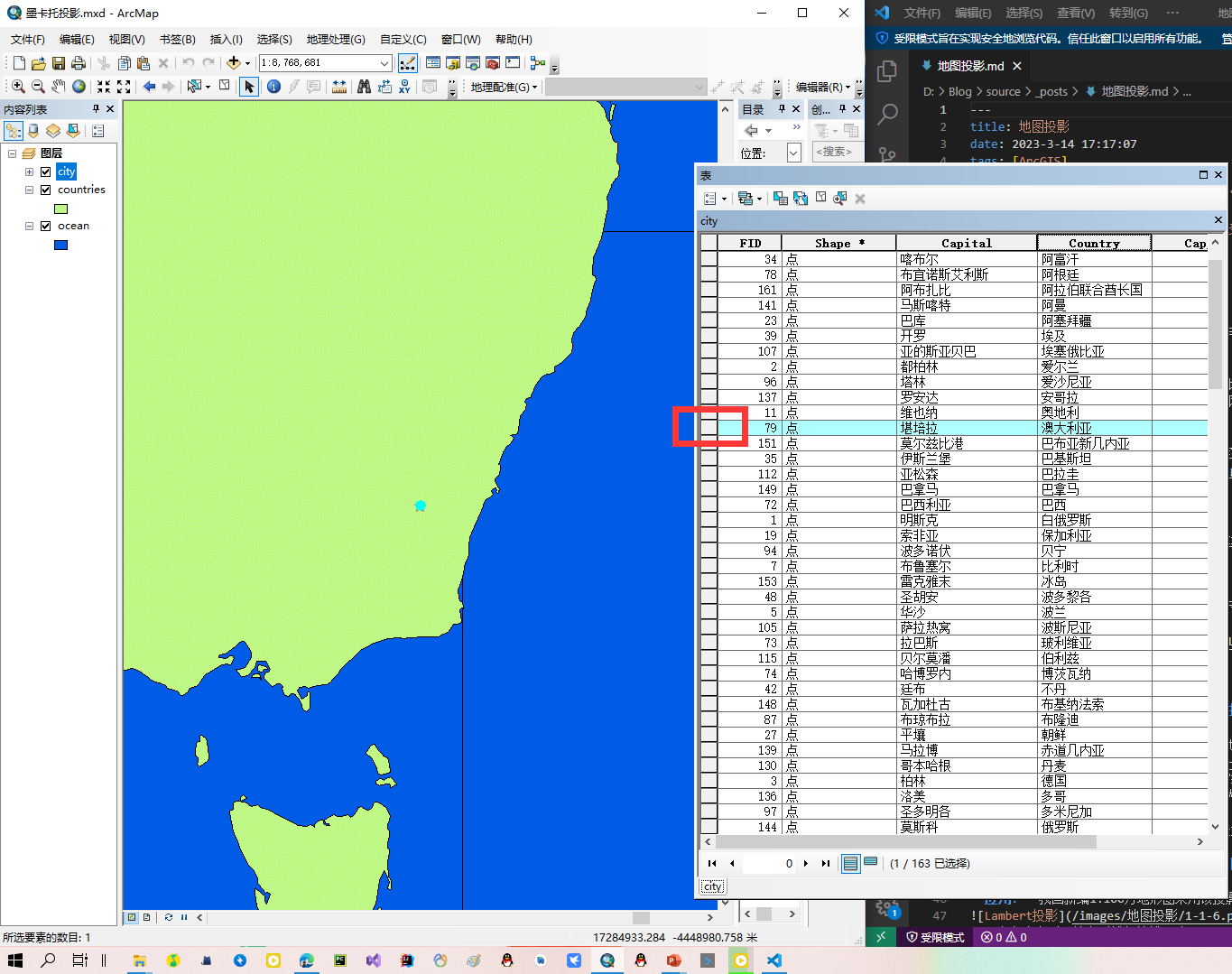
答案
按住ctrl在单机可以多选，这时再看大地图，两地已经被标识出来
使用测量工具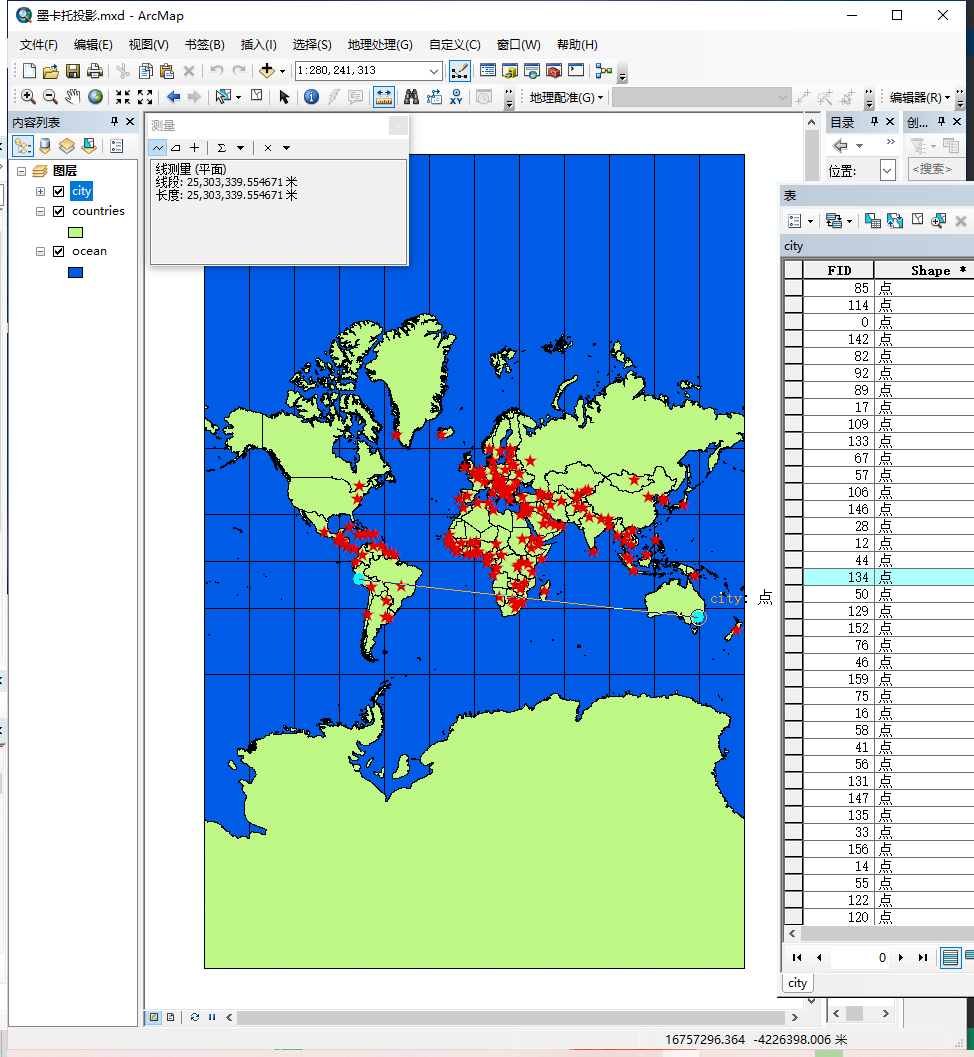
答案

25种地图投影类型

ArcGISPro支持的地图投影

ArcGIS中地图投影实验

实验目的
  • 了解ArcGIS中的地图数据组织和SHP数据格式
  • 了解ArcGIS软件中对于空间参考的定义以及PRJ文件
  • 理解ArcGIS中的动态投影
  • 实践ArcGIS软件中的投影设置工具
  • 实践ArcGIS软件中的投影变换工具

ArcGIS地图数据模型与SHP数据格式

.shp空间数据
.dbf属性数据
.sbx索引文件

格式

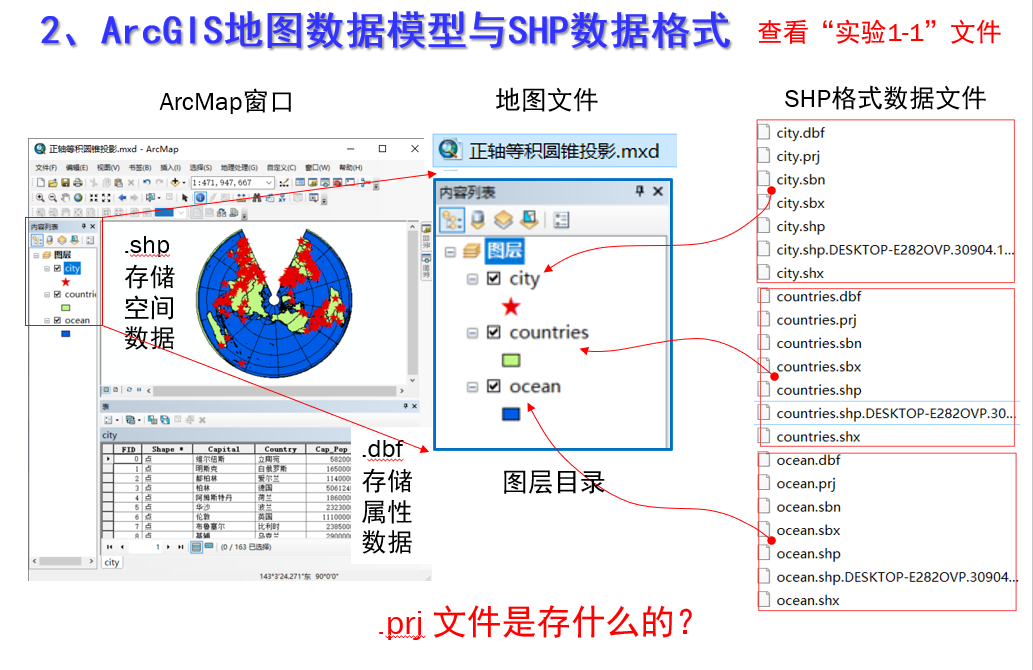
PRJ文件的内容

把.prj用记事本打开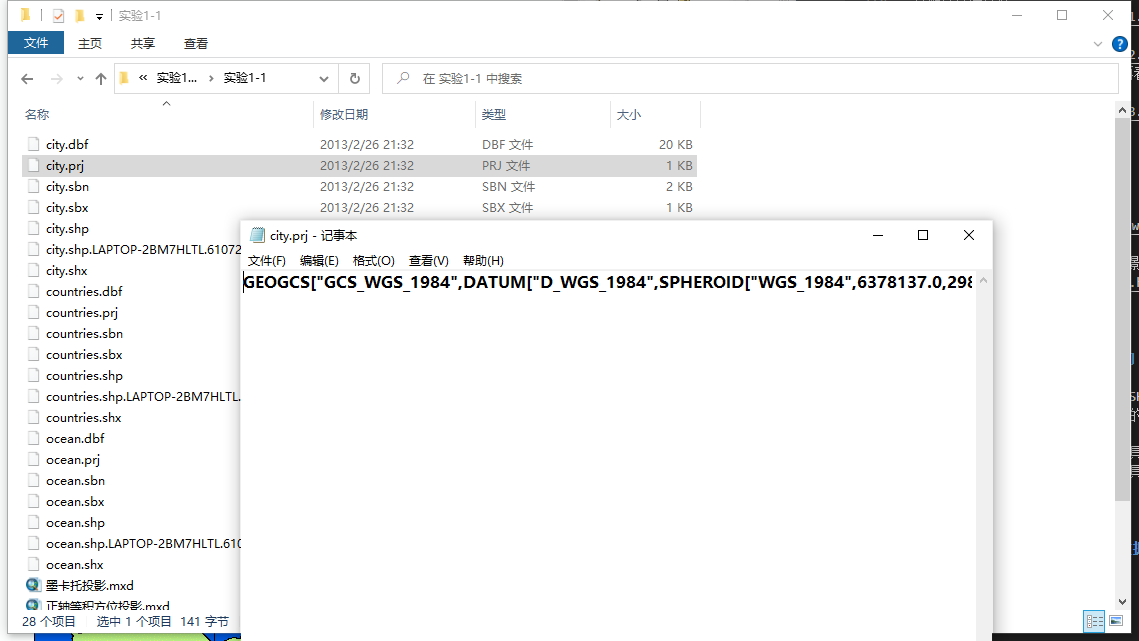
prj
对照图层坐标属性看一下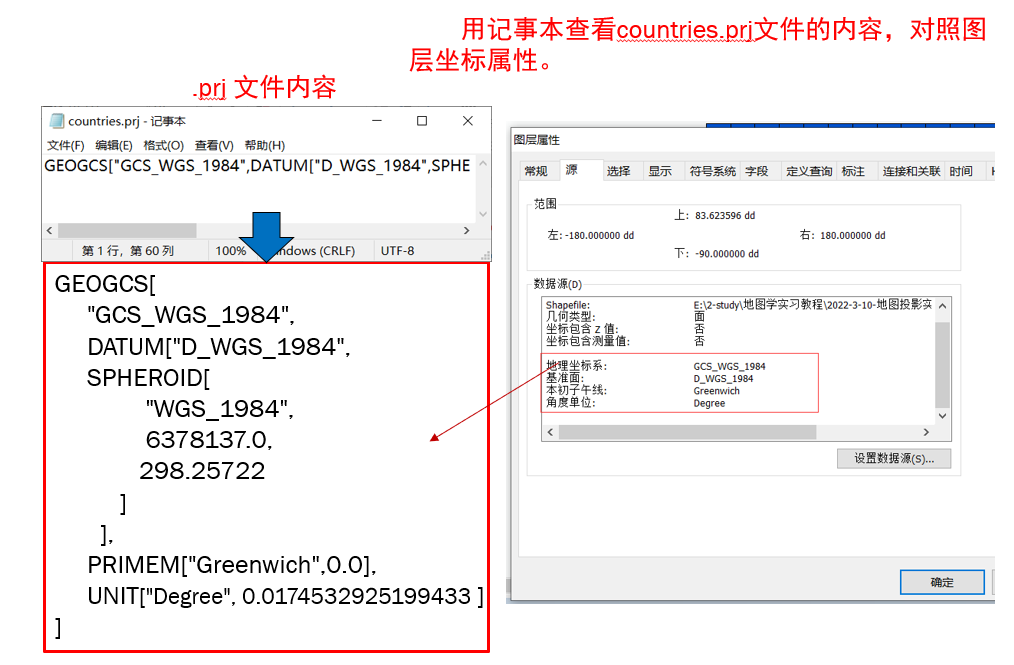
prj
可以看到这里图层的坐标系和数据框的坐标系是不同的，但是他仍然显示为墨卡托投影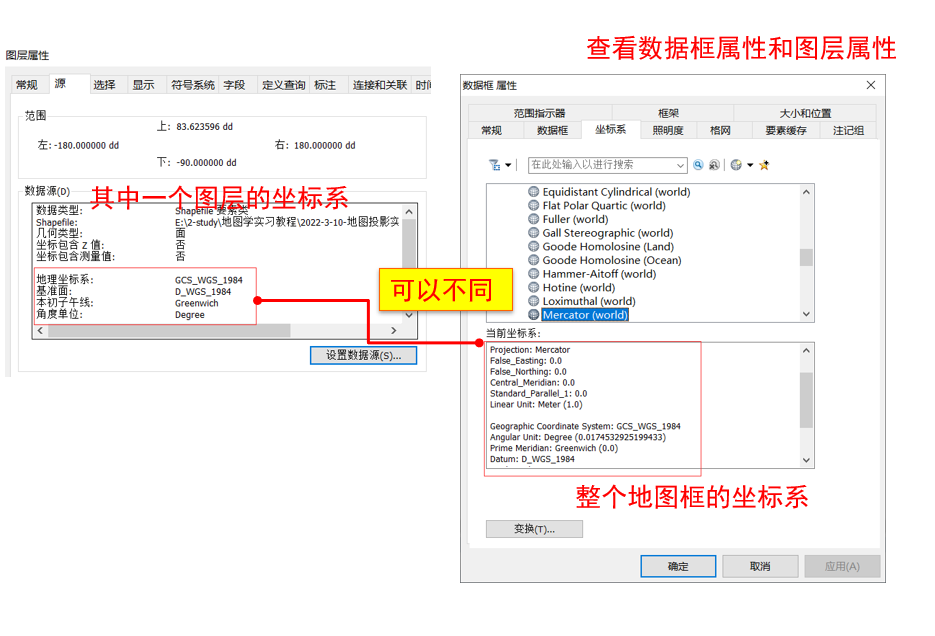
prj
这是因为ArcGIS对数据显示的时候采用了动态投影的过程

动态投影及其设置

如果我们数据框采用了A坐标系统，而我们加进来的数据系统默认的不是A,那么ArcGIS会把后加进来的数据按照地图框的系统进行转换，所以我们放大缩小可以看到地图有“延迟”，这就是再一边转换一边显示，显示每一个点都是动态转换过来的

所以当我们对坐标系进行更改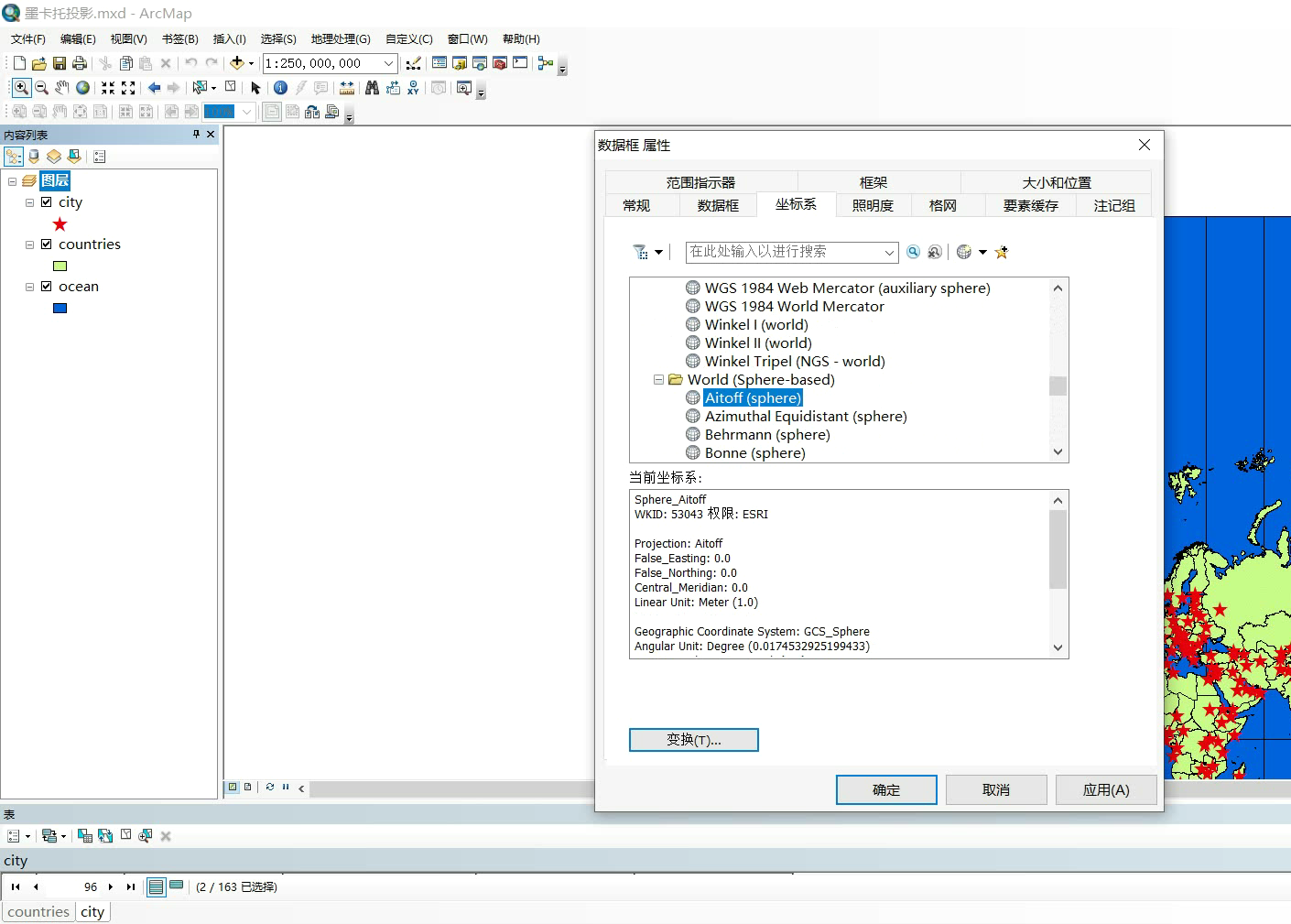
更改坐标系
应用，是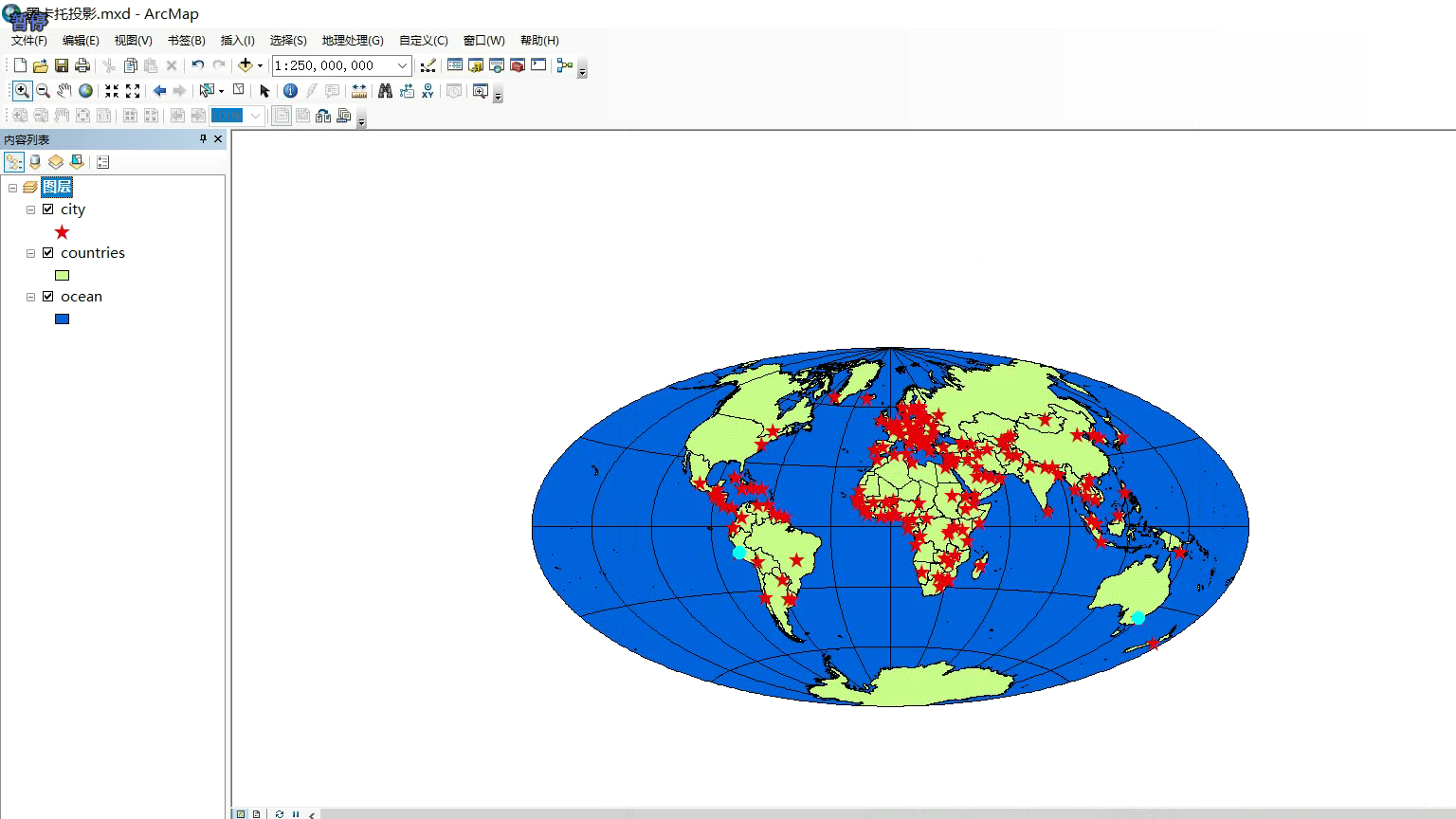
更改坐标系
动态投影就会变成这样

动态投影

动态投影指，ArcMap中的地图数据框的空间参考

  • 默认为第一加载到当前工作区的那个文件的坐标系统
  • 当加入的数据文件的坐标系与之不同时，ArcMap会自动做投影变换，把后加入的数据投影变换到当前坐标系统下显示，但此时数据文件所存储的数据和坐标参数并没有改变

找到投影工具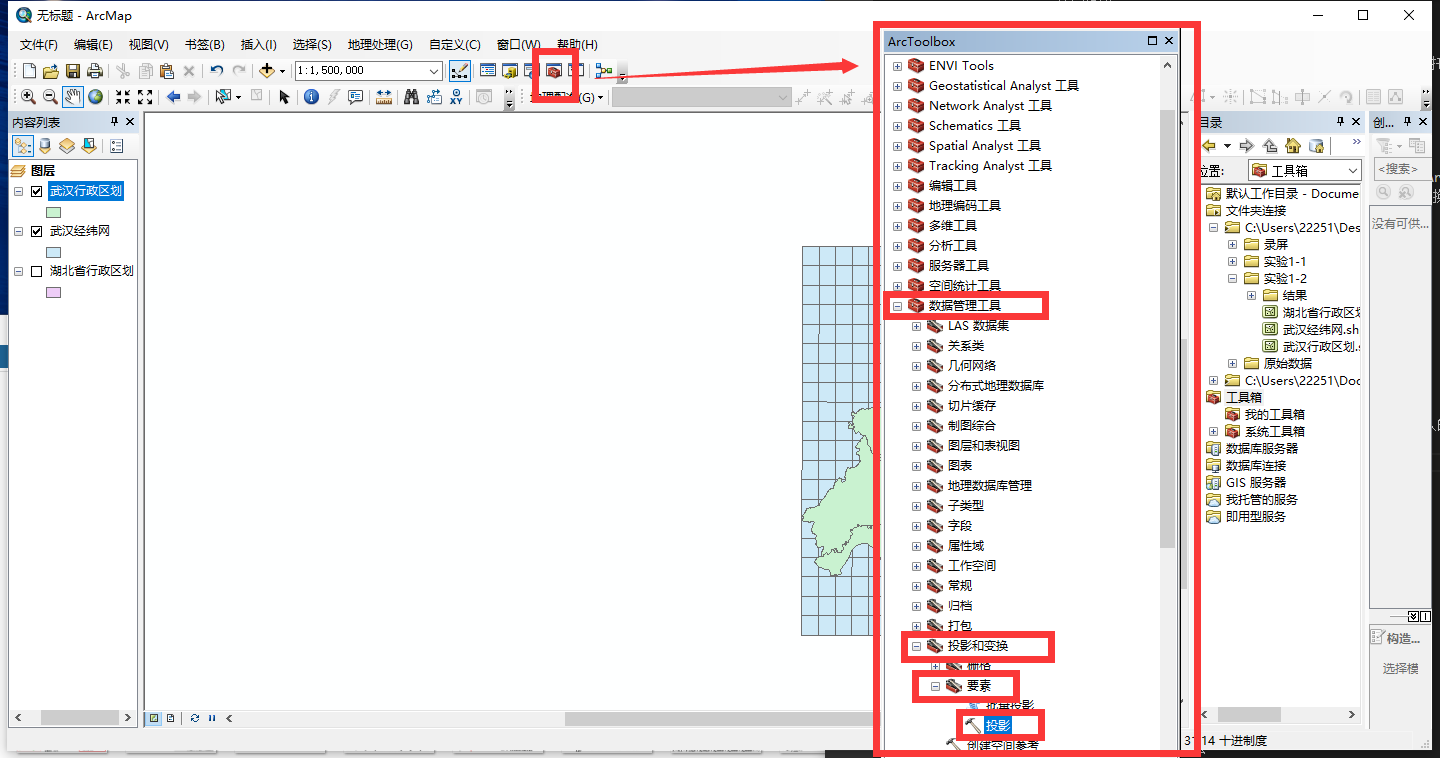
更改坐标系
选择输出坐标系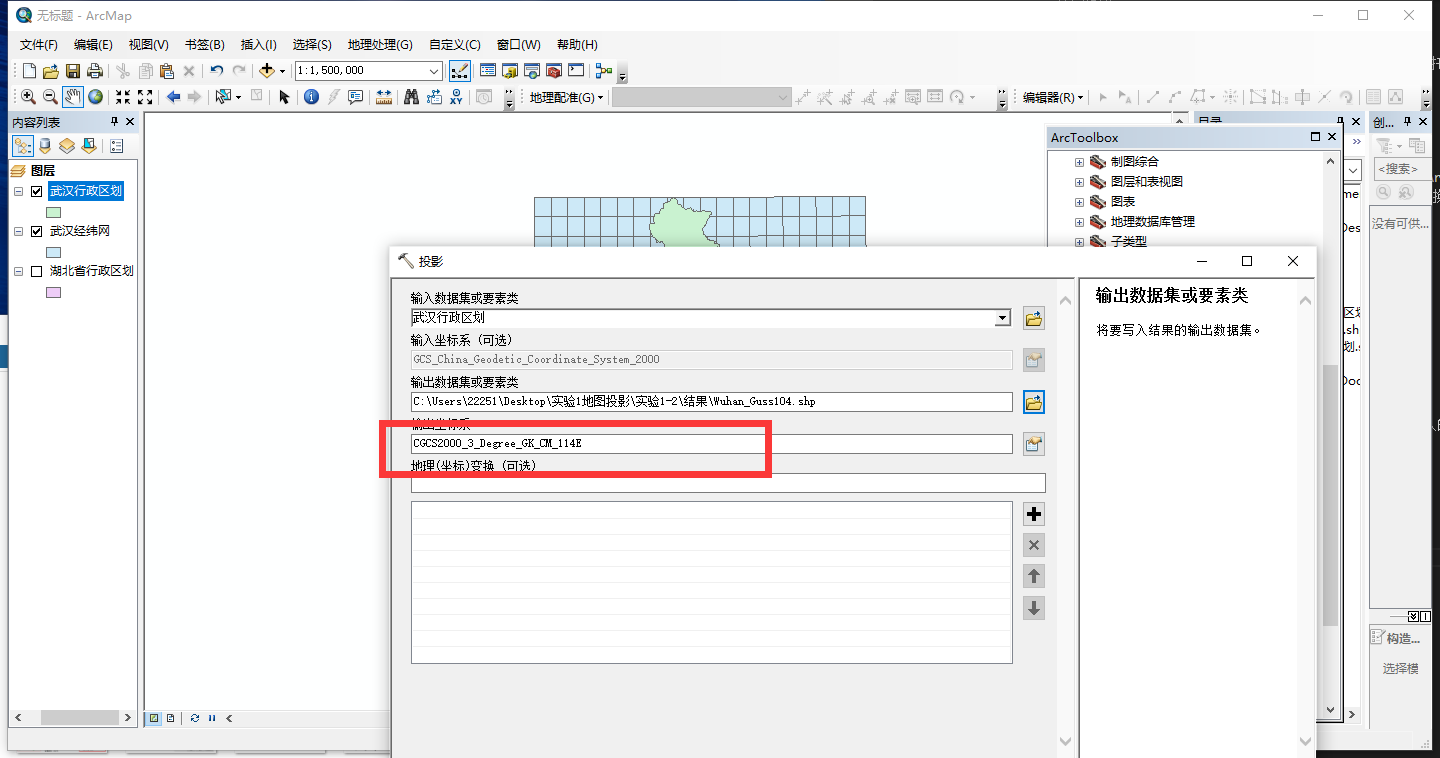
更改坐标系

具体位置 投影坐标系/Gauss Kruger/CGS2000/CGCS2000 3 Degree GK CM 114E

这里下面的地理（坐标）变换 可选不可选是因为这里并不需要做地理坐标变换，假设输入输出之间地理坐标系也不相同，这里就需要做选择怎样转换。

关于选择地理坐标转换

注意看，转换完毕之后的地图自动添加进工作空间了，但是可以发现转换前转换后却完全重叠了
这是因为转换后的地图添加进来之后进行了动态投影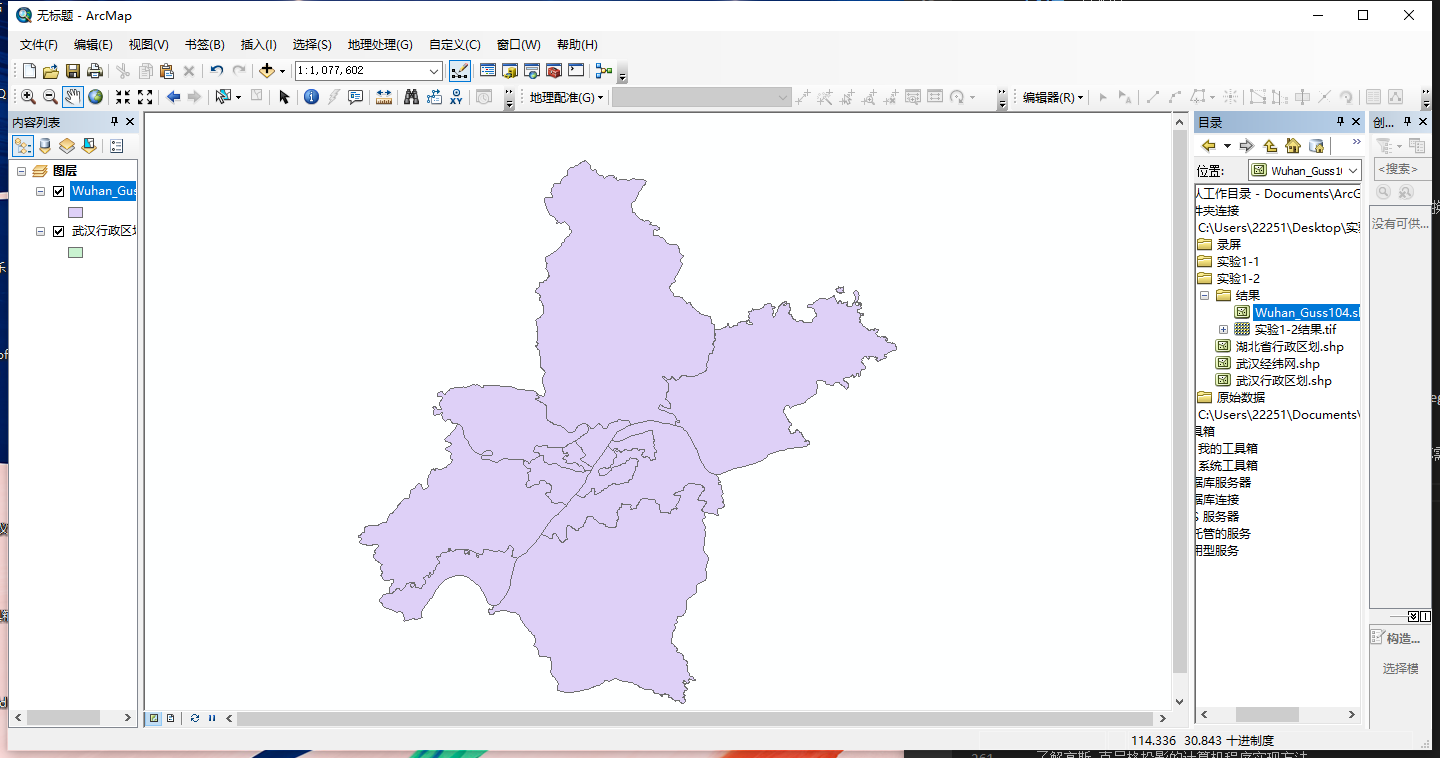
更改坐标系

同样地很轻松就能做出转换成其他坐标系

ArcGIS中的“定义投影”工具

前面说了.prj文件
定义投影实际上就是在改变prj文件，但是仅仅改变了prj文件并没有改变数据对应的值，他肯定会出问题，所以我们一般不用定义投影工具，除非说这个地图文件本来就没有prj文件，我们恰好知道他的对应坐标系是什么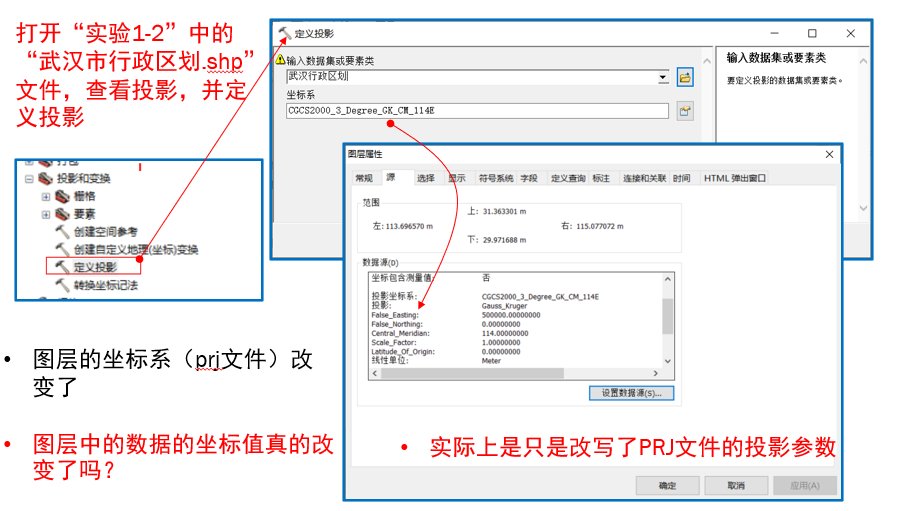
定义投影

ArcGIS中的“投影/批量投影”工具

批量投影

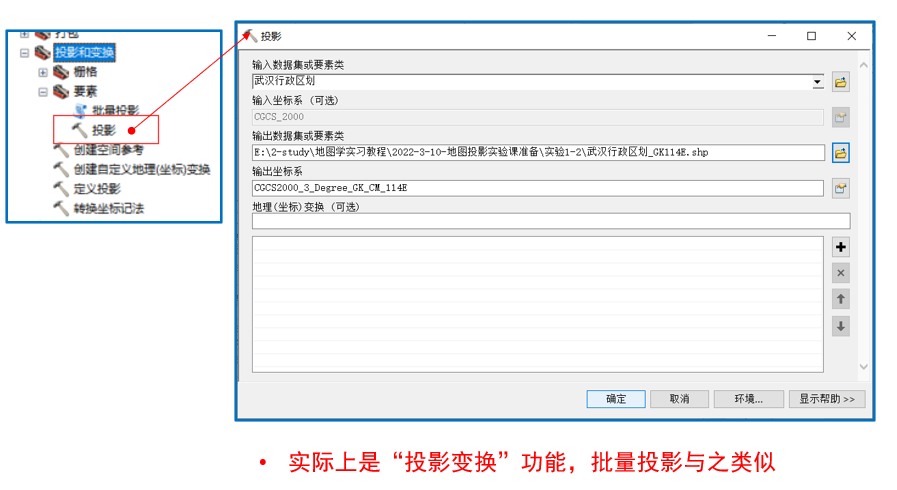
地理坐标系及其转换

前面在讲大地基准的时候我们说是不定的

我们国家常用地理坐标系
  • 北京54
  • 西安80
  • WGS84
  • CGCS2000坐标系
  • 高德火星坐标系GCJ02
  • 百度加密坐标系BD09

他们都是应对不同的需要而建立的，总的来说分为两种

  • 地心基准面（Geocentric datums）
  • 本地基准面（Local datums）

我们之需要地理坐标转换是因为我们在不同的时期应不同的需要，产生了很多的地理坐标系，
这样不同的坐标系的大地基准可能都不一样，我们就需要把他们拿过来整合到一个系统里，这样我们就需要一套地理坐标转换的方法。

正如前面所说地理坐标系转换蛮简单的
只不过这里不是选投影坐标系，而是选地理坐标系

你可以来试一下下面这两个

  • CGCS2000转Beijing1954
  • Bejing1954转Xian1980
当你做到第二个北京54转西安80你可能就会发现有问题

这里会显示“未定义的地理（坐标）变换”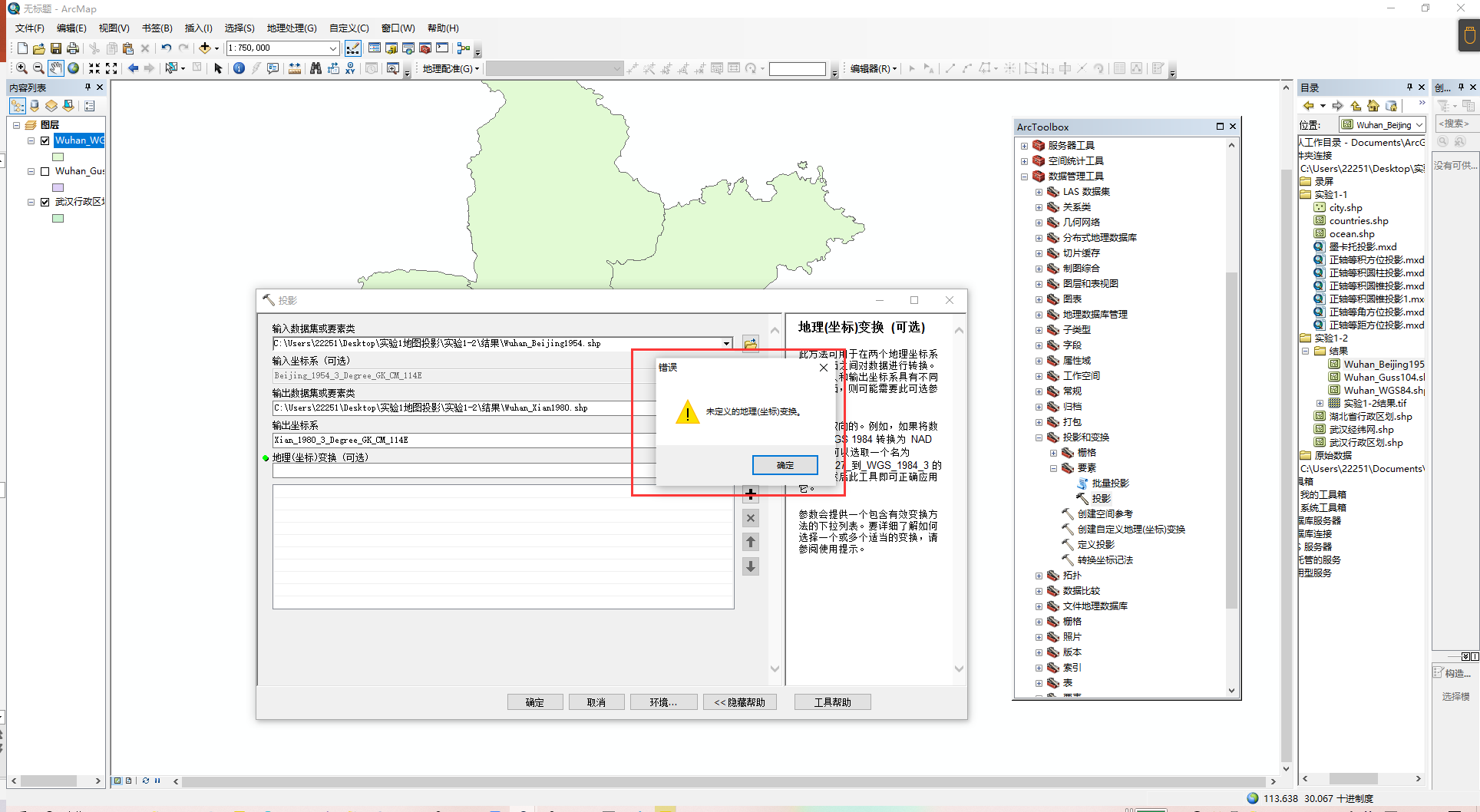
更改坐标系
像前面所说的，这里需要选择转换方式，但是我们并没有北京54转西安80的方法
这里我们就需要自定义坐标转换
工具位置就在前面用的投影工具的下面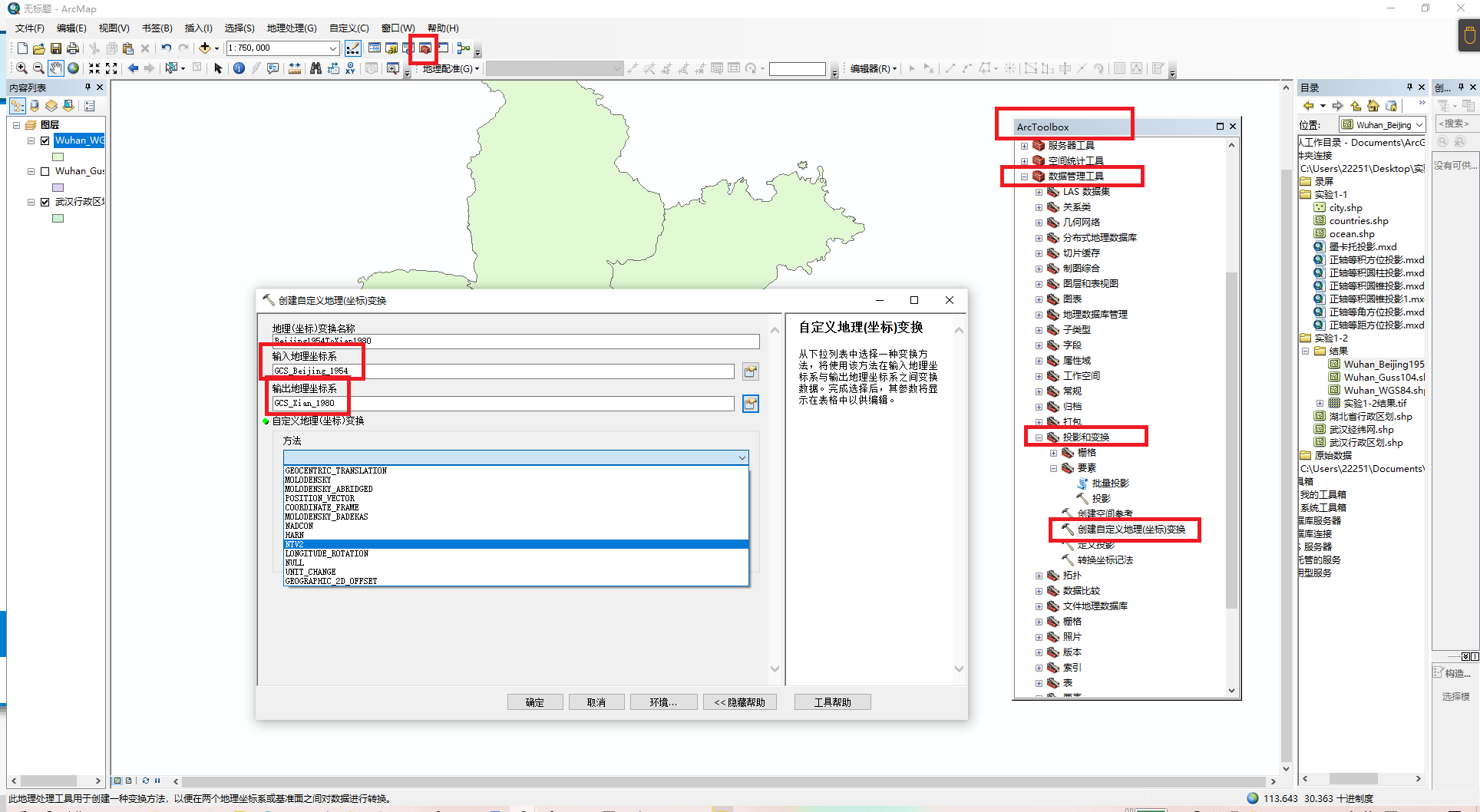
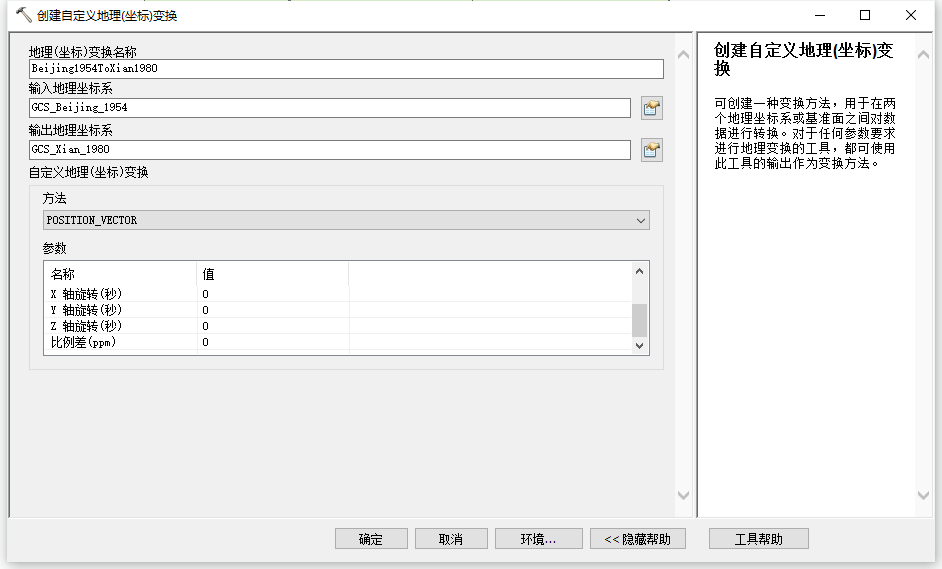
更改坐标系
方法我们就选择COORDINATE_Frame/Position Vector（也就是七参数变换）

七参数坐标转换原理（COORDINATE_FRAME）
  • 如果原点相同，通过三次旋转，就可以两个坐标系重合；
  • 如果原点不同，通过沿三个坐标轴的平移和旋转可以取得一致；
  • 如果两个坐标系的尺度也不尽一致，就需要再增加一个尺度变化参数。

更改坐标系

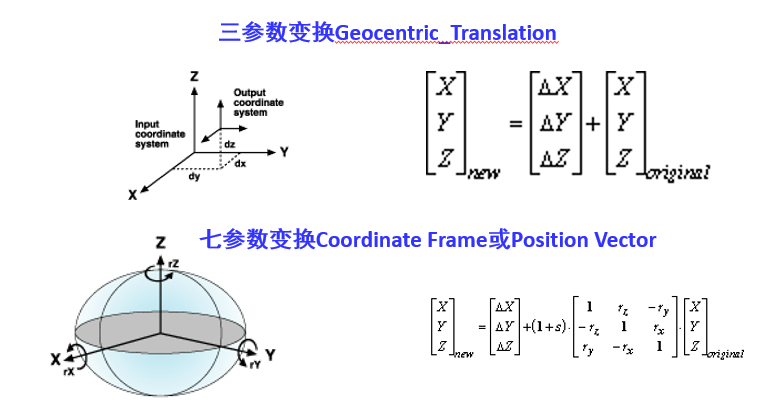
ArcGIS中提供地理变换方法主要有这几种
  • Geocentric_Translation
  • Molodensky
  • Molodensky_Abridged
  • Position_Vector
  • Coordinate_Frame
  • Molodensky_Badekas
  • NADCON
  • HARN
  • NTV2
  • Longitude_Rotation
  • Unit_Change
  • Geographic_2D_Offset
    可使用“创建自定义地理变换（Creat Custom Geographic Transformation）”工具来创建转换方法

三七参转换

ArcGIS种其他投影和变换功能

三七参转换

  • 转换坐标记法工具，用于将包含坐标数据的表格转换为点要素类（Feature Class），且支持多种坐标系下的不同记法

  • 栅格数据的投影变换指将栅格数据集从一种地图投影转换到另一种地图投影，与矢量数据的投影变换原理本质相同。

  • 栅格数据变换是指对数据的平移、扭曲、旋转、翻转、比例、形状、位置的改变等。

投影变换小结

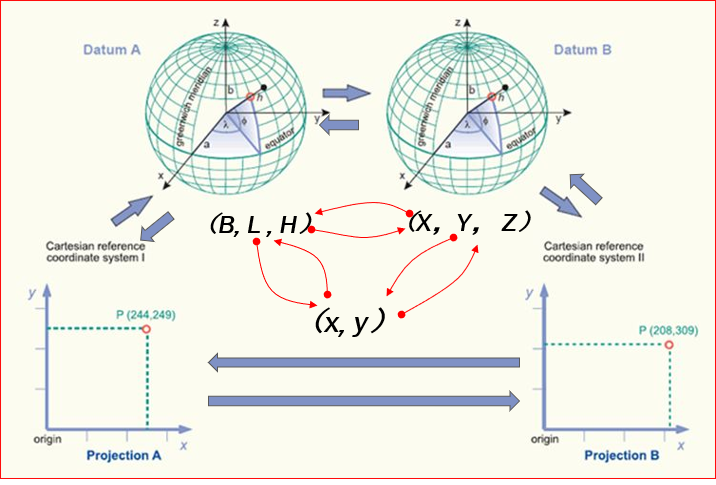
三七参转换

变换形式
  • 地理坐标之间变换
  • 平面坐标之间变换
  • 投影
  • 逆投影
变换方法
  • 解析变换
  • 数值变换
  • 数值-解析变换法
  • 七参数变换

ArcGIS中自定义坐标系

地图投影计算方法实验

实验目的
  • 理解常见投影的数学原理
  • 掌握投影计算方法各种各待定参数的确定方法
  • 了解高斯-克吕格投影的计算机程序实现方法
  • 了解Lambert投影的计算机程序实现方法
  • 了解地图投影的数值变换的计算机程序实现方法

编程环境配置

本章所采用的实习地图数据均来源于“全国地理信息资源目录服务系统”（https://www.webmap.cn/main.do?method=index）数据格式为Shapefile，示例程序采用的编程语言为Python 3， 因此实验中需要采用Python第三方开源库GDAL（https://gdal.org/）对实习中地图数据进行读写。同时也用到了Numpy、Scipy，进行各种数学计算。

GDAL本地安装包的下载路径：

需要根据自己python的版本和操作系统环境下载对应的版本

安装命令：

1
2
cd [GDAL whl文件所在目录]
pip install GDAL-3.4.1-cp37-cp37m-win_amd64.whl

高斯-克吕格投影公式

高斯-克吕格投影计算核心代码

Lambert投影计算公式

地图投影的数值变换计算公式

程序结构说明

投影计算程序测试

作业

https://max.book118.com/html/2017/0428/102896080.shtm

  • 标题: 地图投影
  • 作者: rygdsddssd
  • 创建于 : 2023-03-14 17:17:07
  • 更新于 : 2023-04-01 16:44:44
  • 链接: http://rygdsddssd.github.io/2023/03/14/地图投影/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
 评论
此页目录
地图投影
  1. 地图投影基本概念介绍
    1. 什么是地图学的数学基础？
    2. 大地基准面
    3. 地理坐标系与投影坐标系
    4. 投影的实质和定义
    5. 我国常用地图投影
  2. 地图投影判读实验
    1. 实验目的 掌握地图投影判读的基本方法加深对地图投影的概念、投影变形性质等内容的理解加强对常用地图投影经纬网形状变化特点的了解能够快速判别出地图投影的类别和变形性质
    2. 投影判读的基本方法
    3. 常见投影的基本特征
    4. 地图投影判读作业
  3. ArcGIS中地图投影实验
    1. 实验目的 了解ArcGIS中的地图数据组织和SHP数据格式了解ArcGIS软件中对于空间参考的定义以及PRJ文件理解ArcGIS中的动态投影实践ArcGIS软件中的投影设置工具实践ArcGIS软件中的投影变换工具
    2. ArcGIS地图数据模型与SHP数据格式
    3. PRJ文件的内容
    4. 动态投影及其设置
    5. ArcGIS中的“定义投影”工具
    6. ArcGIS中的“投影/批量投影”工具
    7. 地理坐标系及其转换
    8. ArcGIS种其他投影和变换功能
    9. 投影变换小结
    10. ArcGIS中自定义坐标系
  4. 地图投影计算方法实验
    1. 实验目的 理解常见投影的数学原理掌握投影计算方法各种各待定参数的确定方法了解高斯-克吕格投影的计算机程序实现方法了解Lambert投影的计算机程序实现方法了解地图投影的数值变换的计算机程序实现方法
    2. 编程环境配置
  5. 本章所采用的实习地图数据均来源于“全国地理信息资源目录服务系统”（https://www.webmap.cn/main.do?method=index）数据格式为Shapefile，示例程序采用的编程语言为Python 3， 因此实验中需要采用Python第三方开源库GDAL（https://gdal.org/）对实习中地图数据进行读写。同时也用到了Numpy、Scipy，进行各种数学计算。
    1. 高斯-克吕格投影公式
    2. 高斯-克吕格投影计算核心代码
    3. Lambert投影计算公式
    4. 地图投影的数值变换计算公式
    5. 程序结构说明
    6. 投影计算程序测试
  6. 作业