LINGO软件的初步使用及解读
早上八点上到中午十一点半,休息了5分钟,我要死了。——2023/3/26疲惫不堪的我
例子:牛奶生产

答案代码对照着一看就知道了
1 | max=72*x1+64*x2; |
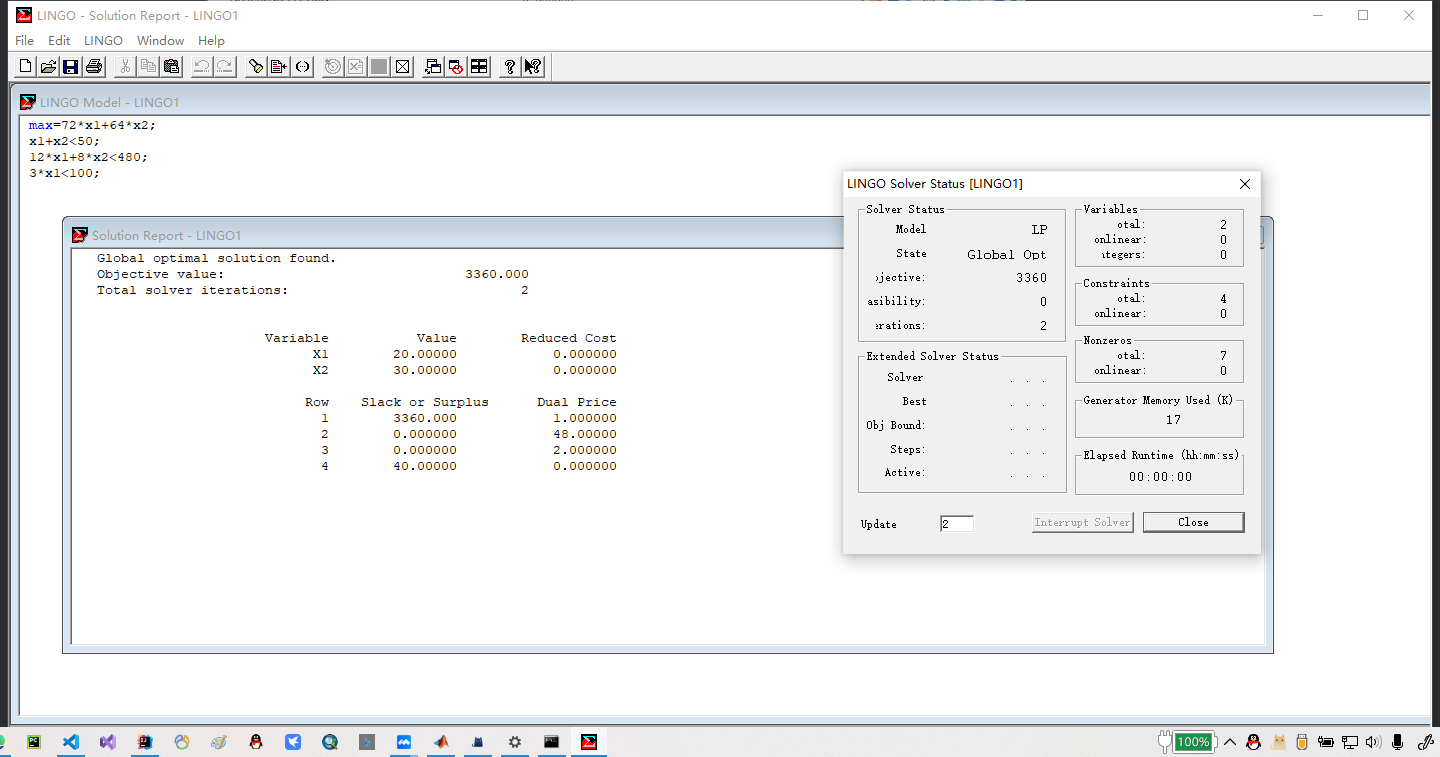
内容解读
内容解读
found
表示全局最优解找到
value
表示最优目标值
iterations
表示用单纯行法进行了两次迭代
Variable
表示变量,运行结果中有两个变量为x1,x2
Value
给出最优解中个变量的值
Cost
与最优单纯形表中的检验数相差一个符号的数。
为了使某个变量在解中的数值增加一个单位,目标函数必须付出的代价(增加或减少Reduced Cost的值)
Surplus
表示接近等于的程度
在约束条件中是<=,叫做松弛变量
在约束条件中是>=,叫做过剩变量
在约束条件中是=,值为0,该约束为一个紧约束(或有效约束)
如果一个约束条件错误,作为一个不可行约束,Slack or Surplus为负数
Slack or Surplus表示的是:约束离相等还差多少
Price
“DUAL PRICE”
(对偶价格)
表示当对应约束有微小变动时,目标函数的变化率。输出结果中对应于每一个约束有一个对偶价格。
若其数值为p,表示对应约束中不等式右端项若增加1个单位,目示函数将增加p个单位(max型问题)。
其实也就是求导
例如在本例中,c约束条件的Dual Price为1,表示2x1+x2<=600增加一个单位到2x1+x2<=601使目标值增加到-1(目标函数的Dual Price为-1),则Objective value就变为799
选址问题

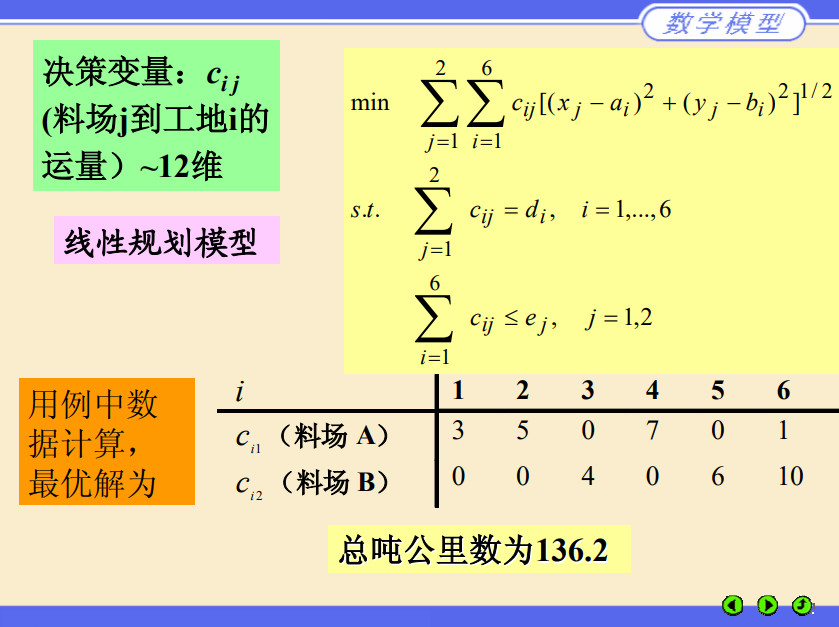
1 | model: |
轰炸任务
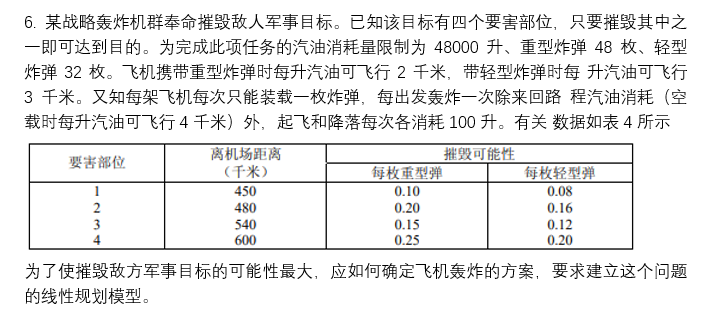
对于这一道题,我先附上我一开始的解法: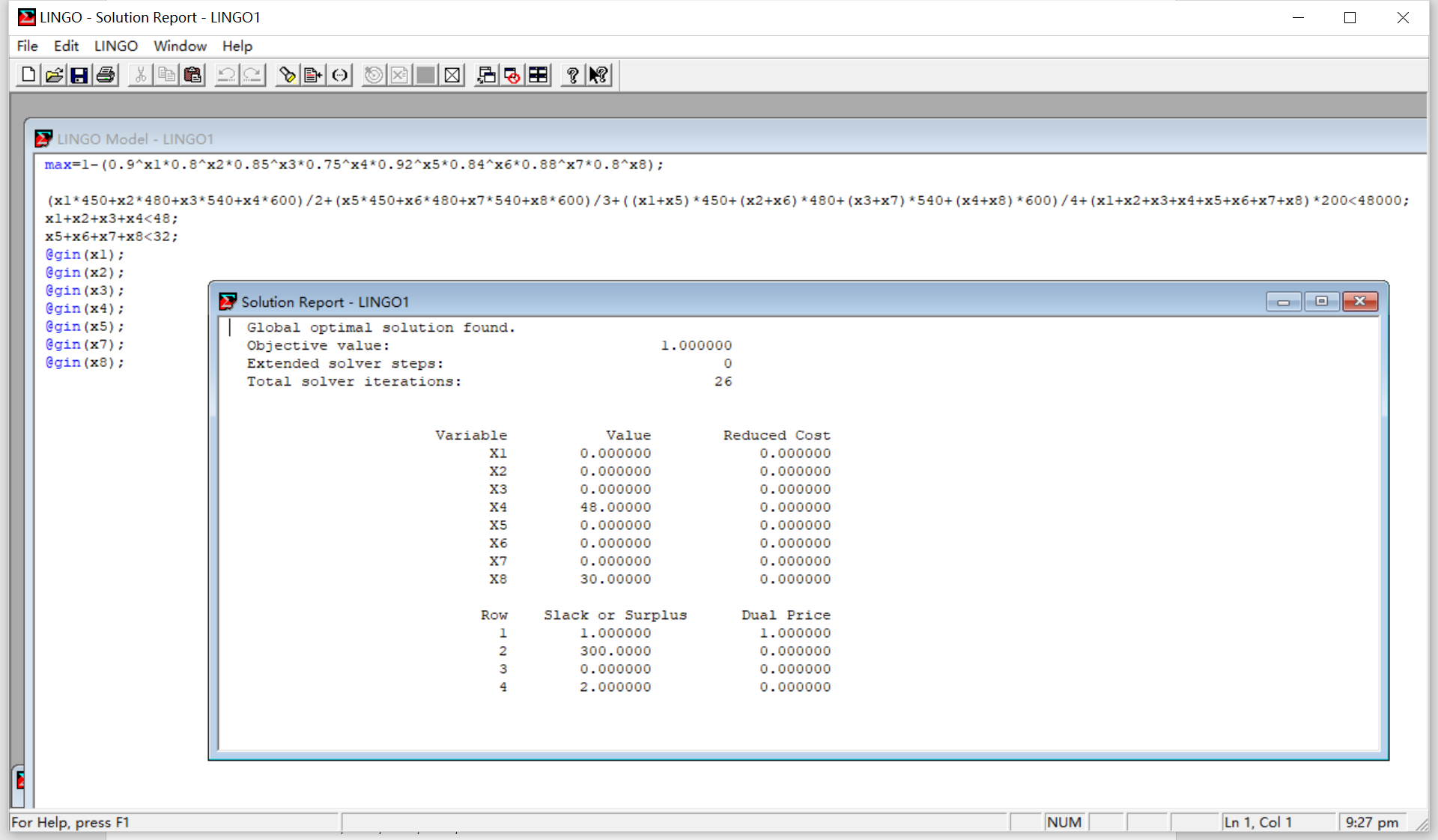
这个做法是有问题的,虽然不是逻辑上的问题。
这是因为在这里目标函数”max”是一个非线性的
1 | max=1-(0.9^x1*0.8^x2*0.85^x3*0.75^x4*0.92^x5*0.84^x6*0.88^x7*0.8^x8); |
而LINGO是用来求解线性规划问题的工具(也可以求解非线性规划,但不能保证得到全局最优解)
所以,
- 要将目标函数改为线性问题
- 使用log
- 限制条件要将所有未知数放在式子左边
修改后代码如下
1 | min=x1*@log(0.9)+x2*@log(0.8)+x3*@log(0.85)+x4*@log(0.75)+x5*@log(0.92)+x6*@log(0.84)+x7*@log(0.88)+x8*@log(0.8); |
运行结果: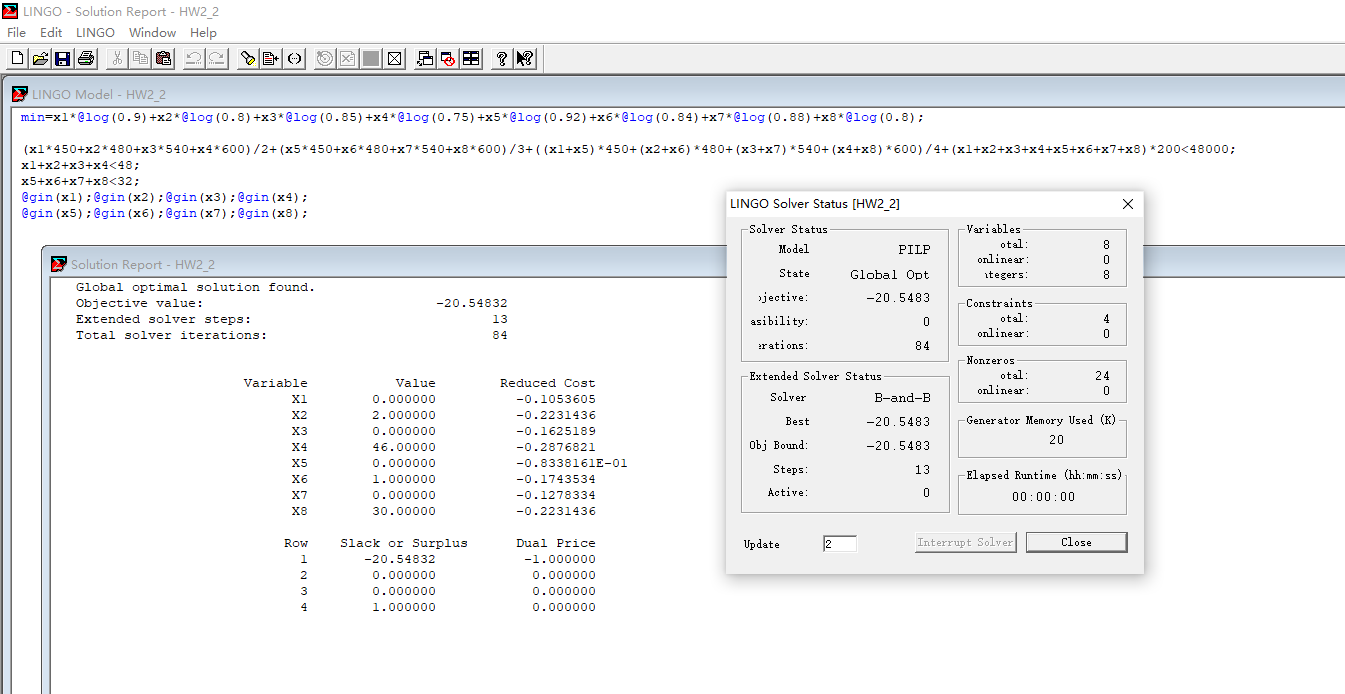
- 标题: LINGO软件的初步使用及解读
- 作者: rygdsddssd
- 创建于 : 2023-03-26 09:40:50
- 更新于 : 2023-04-01 16:44:53
- 链接: http://rygdsddssd.github.io/2023/03/26/LINGO软件的初步使用及解读/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论